Session 5: loglinear regression part 2
Levi Waldron
session_lecture.RmdLearning objectives and outline
Learning objectives
- Define and identify over-dispersion in count data
- Define the negative binomial (NB) distribution and identify applications for it
- Define zero-inflated count models
- Fit and interpret Poisson and NB, with and without zero inflation
Review
Components of GLM
- Random component specifies the conditional distribution for the response variable - it doesn’t have to be normal but can be any distribution that belongs to the “exponential” family of distributions
- Systematic component specifies linear function of predictors (linear predictor)
- Link [denoted by g(.)] specifies the relationship between the expected value of the random component and the systematic component, can be linear or nonlinear
Motivating example: Choice of Distribution
- Count data are often modeled as Poisson distributed:
- mean is greater than 0
- variance is also
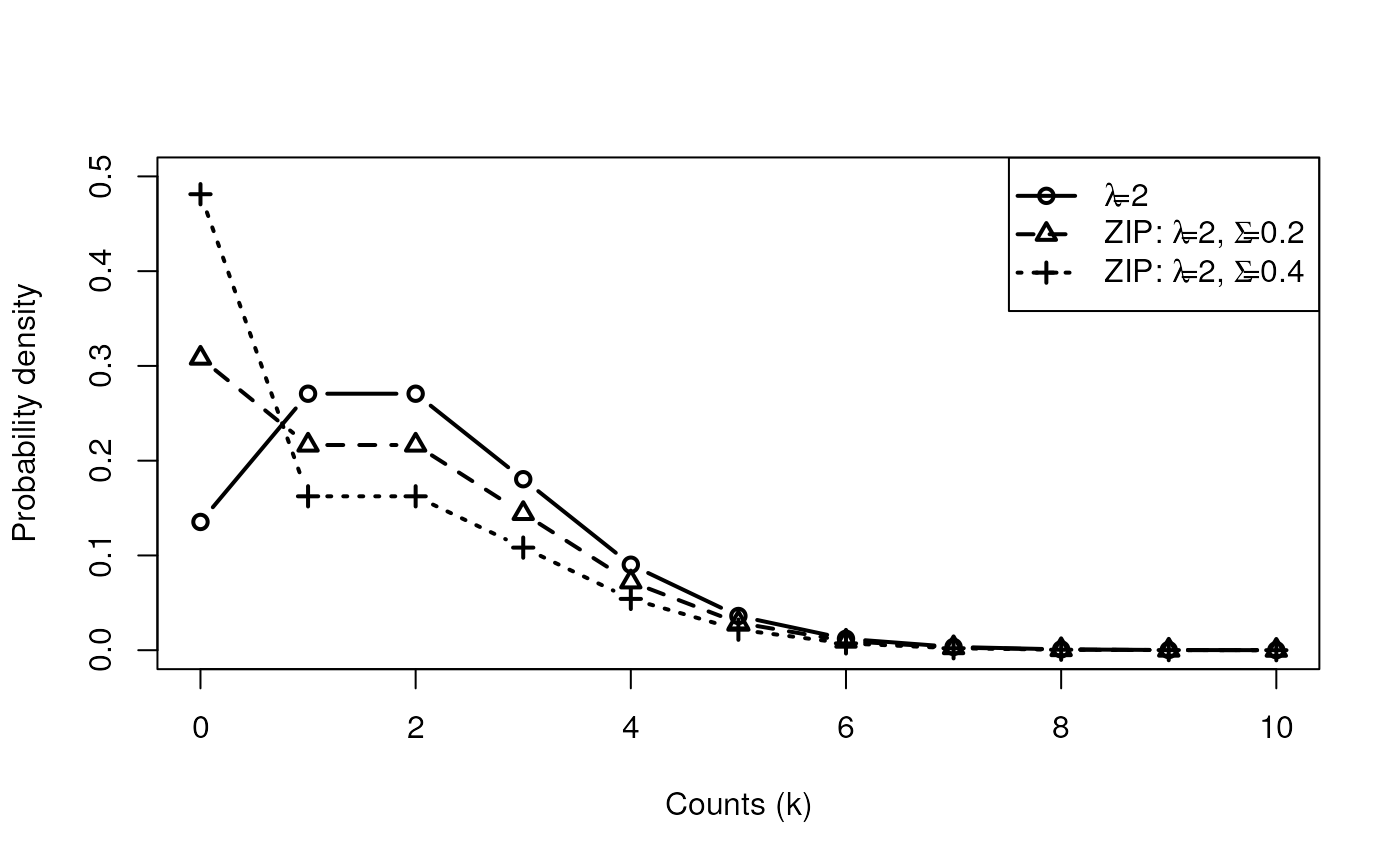
- Probability density
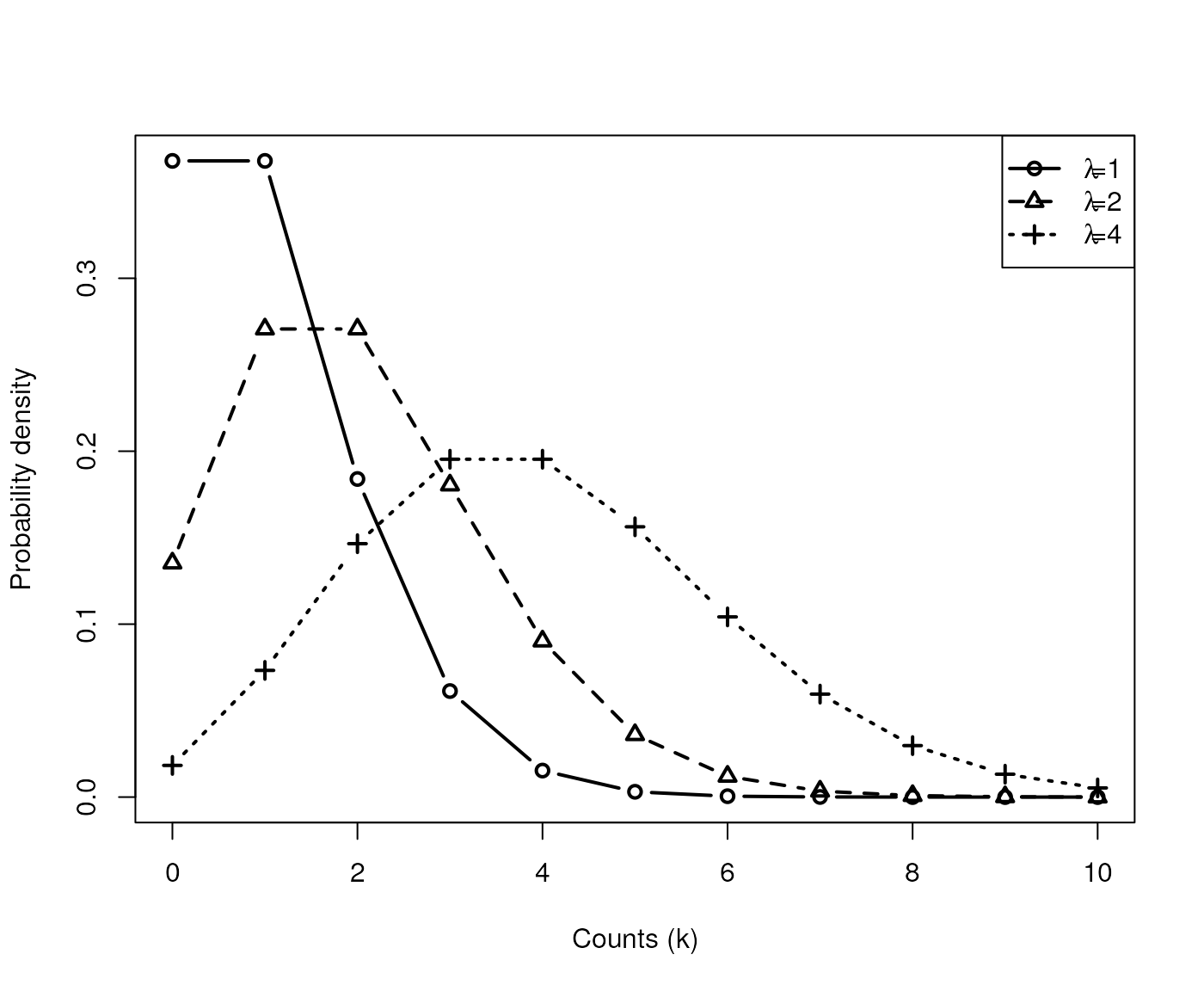
Poisson model: the GLM
The systematic part of the GLM is: Or alternatively:
The random part is (Recall the is both the mean and variance of a Poisson distribution):
Example: Risky Drug Use Behavior
- Outcome is # times the drug user shared a syringe in the past month
(
shared_syr) - Predictors:
sex,ethn,homeless- filtered to
sex“M” or “F”,ethn“White”, “AA”, “Hispanic”
- filtered to
summary(needledat2$shared_syr)## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.000 0.000 0.000 3.122 0.000 60.000 2
var(needledat2$shared_syr, na.rm = TRUE)## [1] 113.371Example: Risky Drug Use Behavior
Exploratory plots

- There are a lot of zeros and variance is much greater than
mean
- Poisson model is probably not a good fit
Over-dispersion
When the Poisson model doesn’t fit
- Variance > mean (over-dispersion)
- Negative binomial distribution
- Excess zeros (zero inflation)
- Can introduce zero-inflation
Negative binomial distribution
- The binomial distribution is the number of successes in n trials:
- Roll a die ten times, how many times do you see a 6?
- The negative binomial distribution is the number of successes it
takes to observe r failures:
- How many times do you have to roll the die to see a 6 ten times?
- Note that the number of rolls is no longer fixed.
- In this example, p=5/6 and a 6 is a “failure”
Negative binomial GLM
One way to parametrize a NB model is with a systematic part equivalent to the Poisson model: Or:
And a random part:
- is a dispersion parameter that is estimated
- When it is equivalent to Poisson model
-
MASS::glm.nb()uses this parametrization,dnbinom()does not - The Poisson model can be considered nested within the Negative Binomial model
Compare Poisson vs. Negative Binomial
Negative Binomial Distribution has two parameters: # of trials n, and probability of success p
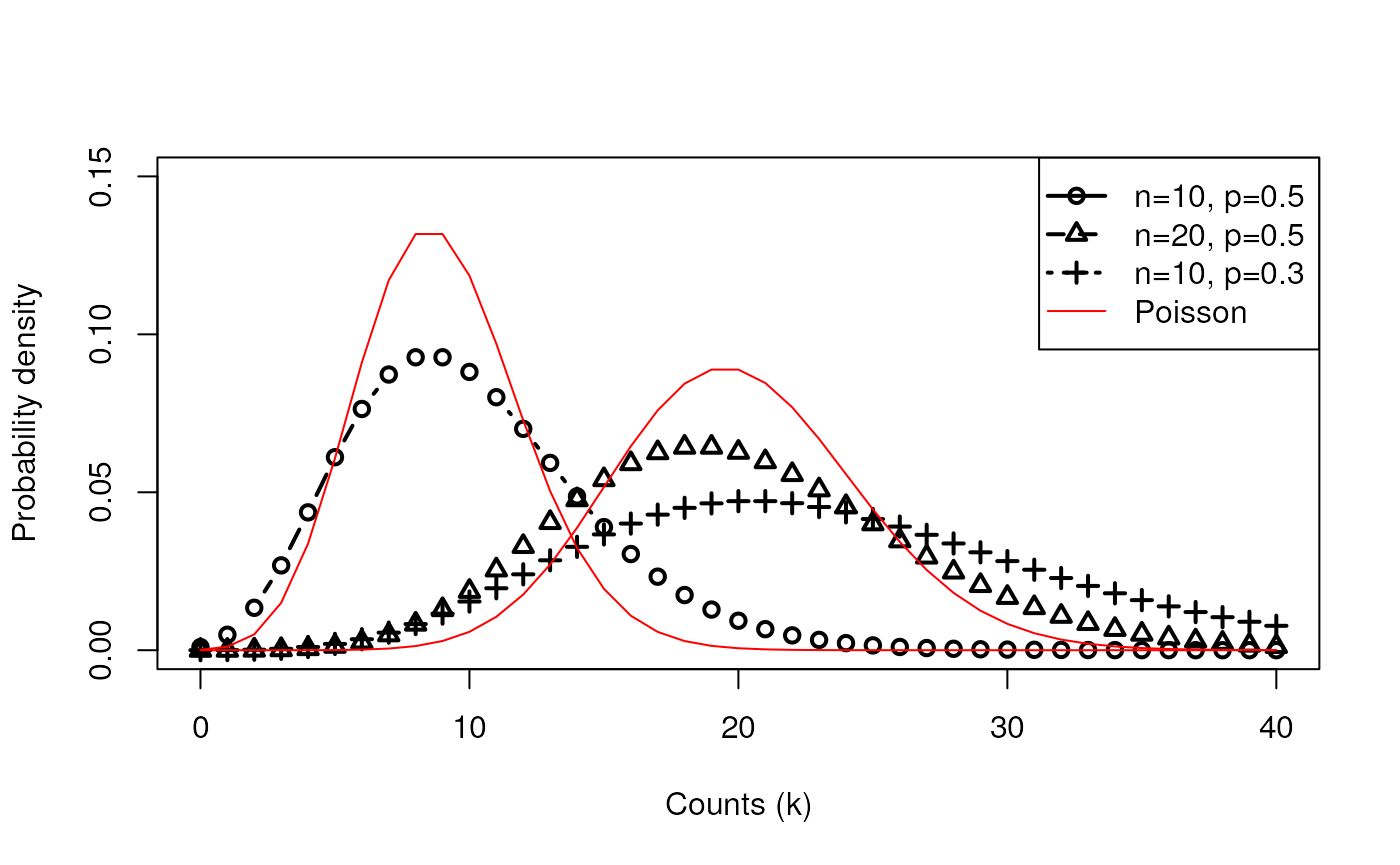
summary(fit.negbin)##
## Call:
## MASS::glm.nb(formula = shared_syr ~ sex + ethn + homeless, data = needledat2,
## init.theta = 0.07743871374, link = log)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.4641 0.8559 0.542 0.5876
## sexM -1.0148 0.8294 -1.224 0.2211
## ethnHispanic 1.3424 1.3201 1.017 0.3092
## ethnWhite 0.2429 0.7765 0.313 0.7544
## homelessyes 1.6445 0.7073 2.325 0.0201 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for Negative Binomial(0.0774) family taken to be 1)
##
## Null deviance: 62.365 on 114 degrees of freedom
## Residual deviance: 56.232 on 110 degrees of freedom
## (2 observations deleted due to missingness)
## AIC: 306.26
##
## Number of Fisher Scoring iterations: 1
##
##
## Theta: 0.0774
## Std. Err.: 0.0184
##
## 2 x log-likelihood: -294.2550Likelihood ratio test
Basis: Under : no improvement in fit by more complex model, difference in model residual deviances is -distributed.
Deviance:
(ll.negbin <- logLik(fit.negbin))## 'log Lik.' -147.1277 (df=6)
(ll.pois <- logLik(fit.pois))## 'log Lik.' -730.0133 (df=5)
pchisq(2 * (ll.negbin - ll.pois), df=1,
lower.tail=FALSE)## 'log Lik.' 1.675949e-255 (df=6)Zero Inflation
Zero inflated “two-step” models
Step 1: logistic model to determine whether count is zero or Poisson/NB
Step 2: Poisson or NB regression distribution for not set to zero by 1.
summary(fit.ZIpois)##
## Call:
## pscl::zeroinfl(formula = shared_syr ~ sex + ethn + homeless, data = needledat2,
## dist = "poisson")
##
## Pearson residuals:
## Min 1Q Median 3Q Max
## -1.0761 -0.5784 -0.4030 -0.3341 10.6835
##
## Count model coefficients (poisson with log link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 3.2169 0.1796 17.909 < 2e-16 ***
## sexM -1.4725 0.1442 -10.212 < 2e-16 ***
## ethnHispanic -0.1525 0.1576 -0.968 0.333223
## ethnWhite -0.5236 0.1464 -3.577 0.000347 ***
## homelessyes 1.2034 0.1455 8.268 < 2e-16 ***
##
## Zero-inflation model coefficients (binomial with logit link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.06262 0.65227 3.162 0.00157 **
## sexM -0.05067 0.58252 -0.087 0.93068
## ethnHispanic -1.76120 0.81177 -2.170 0.03004 *
## ethnWhite -0.50187 0.56919 -0.882 0.37792
## homelessyes -0.53013 0.48108 -1.102 0.27048
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Number of iterations in BFGS optimization: 18
## Log-likelihood: -299.8 on 10 DfZero-inflated Negative Binomial regression
fit.ZInegbin <-
pscl::zeroinfl(shared_syr~sex+ethn+homeless,
dist = "negbin",
data = needledat2)- NOTE: zero-inflation model can include any of your variables as predictors
-
WARNING Default in
zerinfl()function is to use all variables as predictors in logistic model
summary(fit.ZInegbin)##
## Call:
## pscl::zeroinfl(formula = shared_syr ~ sex + ethn + homeless, data = needledat2,
## dist = "negbin")
##
## Pearson residuals:
## Min 1Q Median 3Q Max
## -0.5401 -0.3255 -0.2715 -0.1926 5.1489
##
## Count model coefficients (negbin with log link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.8401 1.1845 2.398 0.01649 *
## sexM -2.2278 0.9350 -2.382 0.01720 *
## ethnHispanic -0.4116 0.9832 -0.419 0.67545
## ethnWhite -0.4294 0.8647 -0.497 0.61949
## homelessyes 1.9461 0.7103 2.740 0.00615 **
## Log(theta) -1.1972 0.5159 -2.320 0.02032 *
##
## Zero-inflation model coefficients (binomial with logit link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.6863 0.8466 1.992 0.0464 *
## sexM -0.9919 0.8016 -1.237 0.2159
## ethnHispanic -11.3556 112.8675 -0.101 0.9199
## ethnWhite -0.7452 0.7304 -1.020 0.3076
## homelessyes 0.3555 0.7397 0.481 0.6308
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Theta = 0.302
## Number of iterations in BFGS optimization: 37
## Log-likelihood: -142.8 on 11 DfZero-inflated NB - simplified
- Model is much more interpretable if the exposure of interest is not included in the zero-inflation model.
- E.g. with HIV status as the only predictor in zero-inflation model:
fit.ZInb2 <- pscl::zeroinfl(shared_syr ~ sex + ethn +
homeless + hiv | hiv,
dist = "negbin",
data = needledat2)
summary(fit.ZInb2)##
## Call:
## pscl::zeroinfl(formula = shared_syr ~ sex + ethn + homeless + hiv | hiv,
## data = needledat2, dist = "negbin")
##
## Pearson residuals:
## Min 1Q Median 3Q Max
## -0.4299 -0.3646 -0.3559 -0.3299 6.3053
##
## Count model coefficients (negbin with log link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 3.6685 0.9470 3.874 0.000107 ***
## sexM -1.7648 0.6205 -2.844 0.004454 **
## ethnHispanic -1.5808 0.7446 -2.123 0.033757 *
## ethnWhite -1.1268 0.6924 -1.627 0.103662
## homelessyes 1.0313 0.5692 1.812 0.070025 .
## hivpositive -1.0820 1.0167 -1.064 0.287245
## hivyes 2.3723 0.7829 3.030 0.002443 **
## Log(theta) 0.1396 0.4647 0.300 0.763941
##
## Zero-inflation model coefficients (binomial with logit link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.2163 0.2851 4.266 1.99e-05 ***
## hivpositive -0.3493 0.9389 -0.372 0.710
## hivyes -17.9654 3065.6162 -0.006 0.995
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Theta = 1.1498
## Number of iterations in BFGS optimization: 59
## Log-likelihood: -122.5 on 11 DfIntercept-only ZI model
fit.ZInb3 <-
pscl::zeroinfl(shared_syr~sex+ethn+homeless|1,
dist = "negbin",
data = needledat2)
summary(fit.ZInb3)##
## Call:
## pscl::zeroinfl(formula = shared_syr ~ sex + ethn + homeless | 1, data = needledat2,
## dist = "negbin")
##
## Pearson residuals:
## Min 1Q Median 3Q Max
## -0.3159 -0.3123 -0.3040 -0.2953 5.2941
##
## Count model coefficients (negbin with log link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.08551 1.42665 1.462 0.1438
## sexM -1.43812 0.89188 -1.612 0.1069
## ethnHispanic 0.48126 1.16639 0.413 0.6799
## ethnWhite -0.07421 0.81066 -0.092 0.9271
## homelessyes 1.62076 0.67705 2.394 0.0167 *
## Log(theta) -1.12533 0.89365 -1.259 0.2079
##
## Zero-inflation model coefficients (binomial with logit link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.5211 0.7599 0.686 0.493
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Theta = 0.3245
## Number of iterations in BFGS optimization: 37
## Log-likelihood: -146.8 on 7 DfConfidence intervals
Use the confint() function for all these models (don’t
try to specify which package confint comes from). E.g.:
confint(fit.ZInb3)## 2.5 % 97.5 %
## count_(Intercept) -0.7106815 4.8816948
## count_sexM -3.1861734 0.3099239
## count_ethnHispanic -1.8048157 2.7673339
## count_ethnWhite -1.6630653 1.5146489
## count_homelessyes 0.2937556 2.9477604
## zero_(Intercept) -0.9683324 2.0105711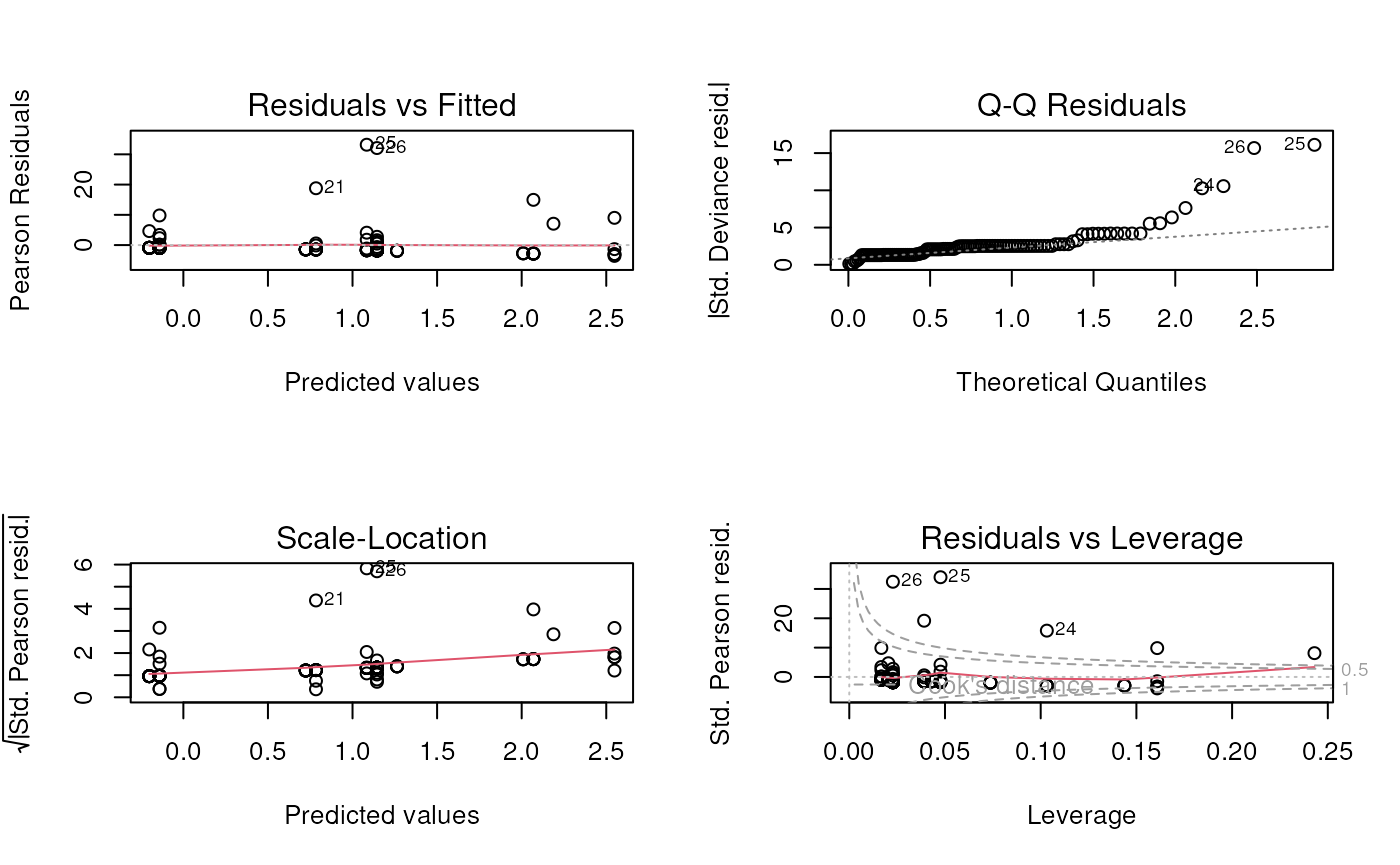 * Poisson model is definitely not a good fit.
* Poisson model is definitely not a good fit.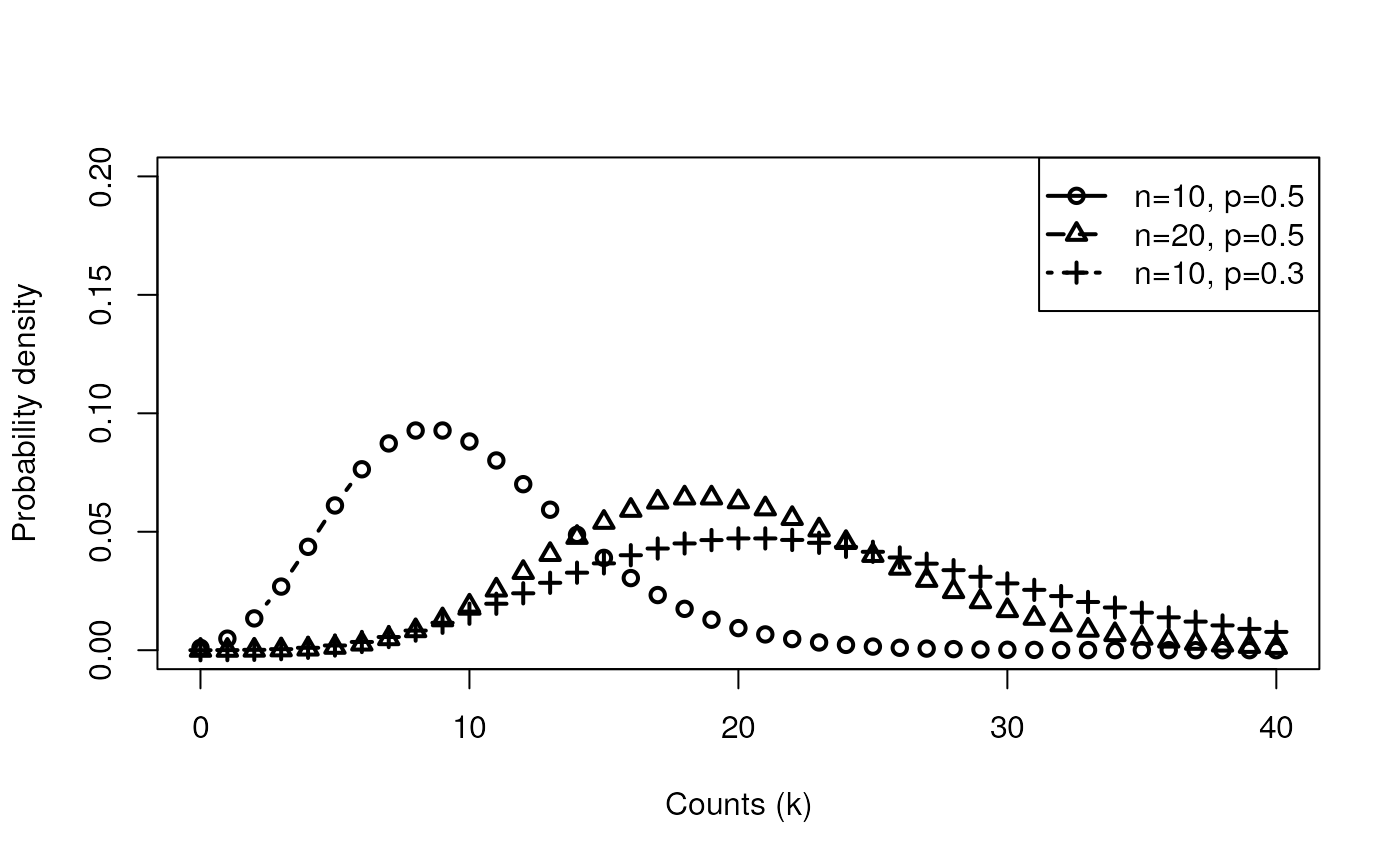
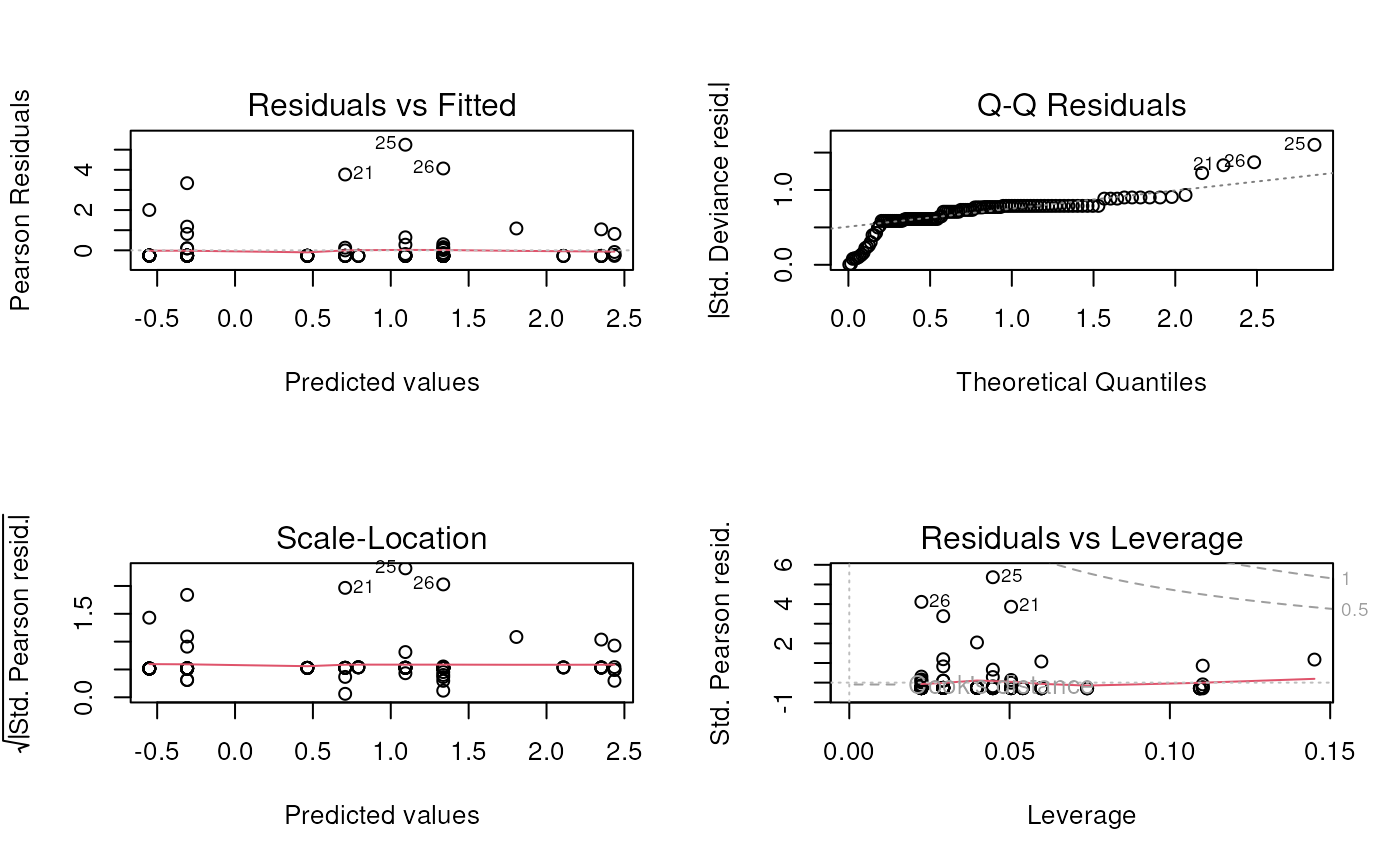
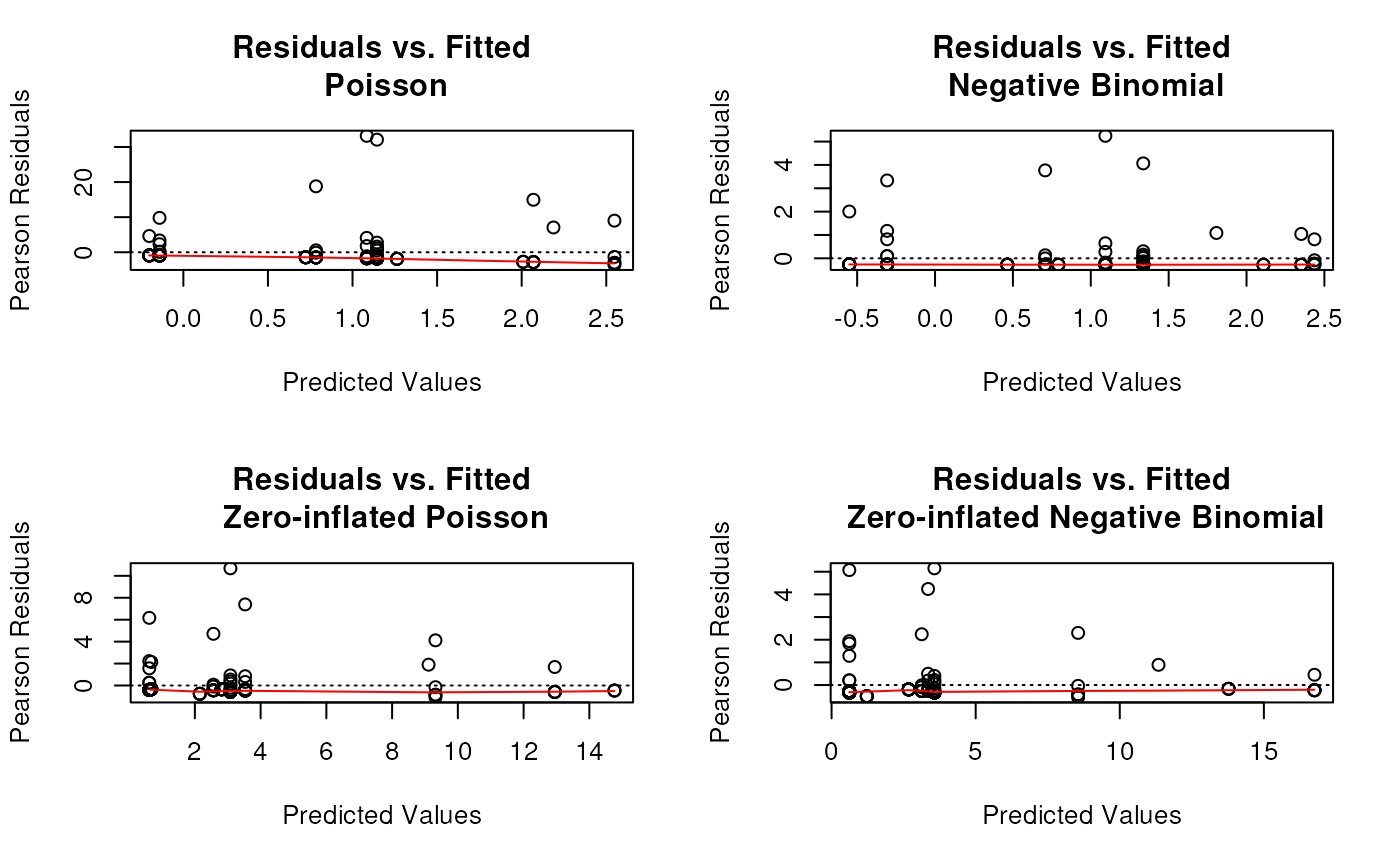
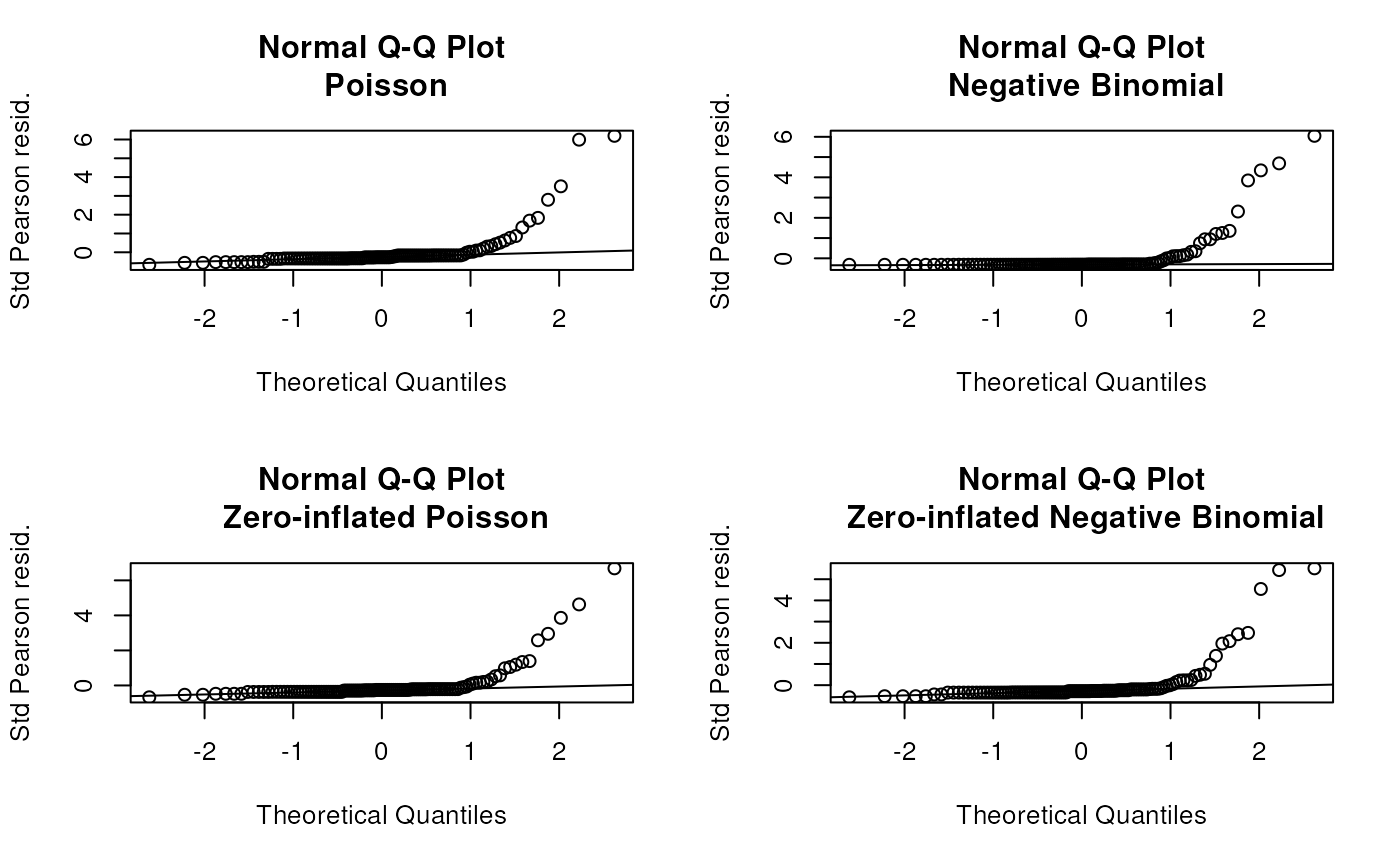 still over-dispersed - ideas?
still over-dispersed - ideas?