Session 5 lab exercise: loglinear regression part 2

Learning objectives

Fit Poisson, NB, and zero-inflated loglinear models
Perform nested deviance test for model selection
Make diagnostic plots of loglinear models
Visually assess multicollinearity among predictors

suppressPackageStartupMessages({
  library(tidyverse)
})
needledat <- readr::read_csv("needle_sharing.csv")
needledat2 <- needledat %>%
  dplyr::filter(sex %in% c("M", "F") &
                  ethn %in% c("White", "AA", "Hispanic") &
                  !is.na(homeless)) %>%
  mutate(
    homeless = recode_factor(homeless, "0" = "no", "1" = "yes"),
    hiv = recode_factor(
      hivstat,
      "0" = "negative",
      "1" = "positive",
      "2" = "positive"
    )
  )

Compare the mean to the variance of the outcome variable. Calculate what fraction of the counts are zero.

meanvarzeros <- filter(needledat2,!is.na(shared_syr)) %>%
  summarise(
    mean = mean(shared_syr),
    var = var(shared_syr),
    fraczero = sum(shared_syr == 0) / n()
  )
meanvarzeros

## # A tibble: 1 × 3
##    mean   var fraczero
##   <dbl> <dbl>    <dbl>
## 1  3.12  113.    0.774

The mean number of needle sharing events per participant is 3.12, the variance is 113, and the fraction of participants who never shared a needle is 0.774. (Note how I put computed results in the text here rather than writing in numbers manually - they will change automatically if the analysis is changed!)

Create a histogram of the outcome variable.

This was done in the lecture using base R, but let’s do it here with ggplot2. Note the filtering of complete cases only is unnecessary because ggplot does it anyways, but this gets rid of a warning (try it without filtering). Specifying the binwidth is also unnecessary, but by default geom_histogram creates histogram bins of size 2 (ie 0 and 1 in the same bin, 2 and 3 together, …)

library(ggplot2)
filter(needledat2, !is.na(shared_syr)) %>%
  ggplot(aes(x = shared_syr)) +
  geom_histogram(binwidth = 1)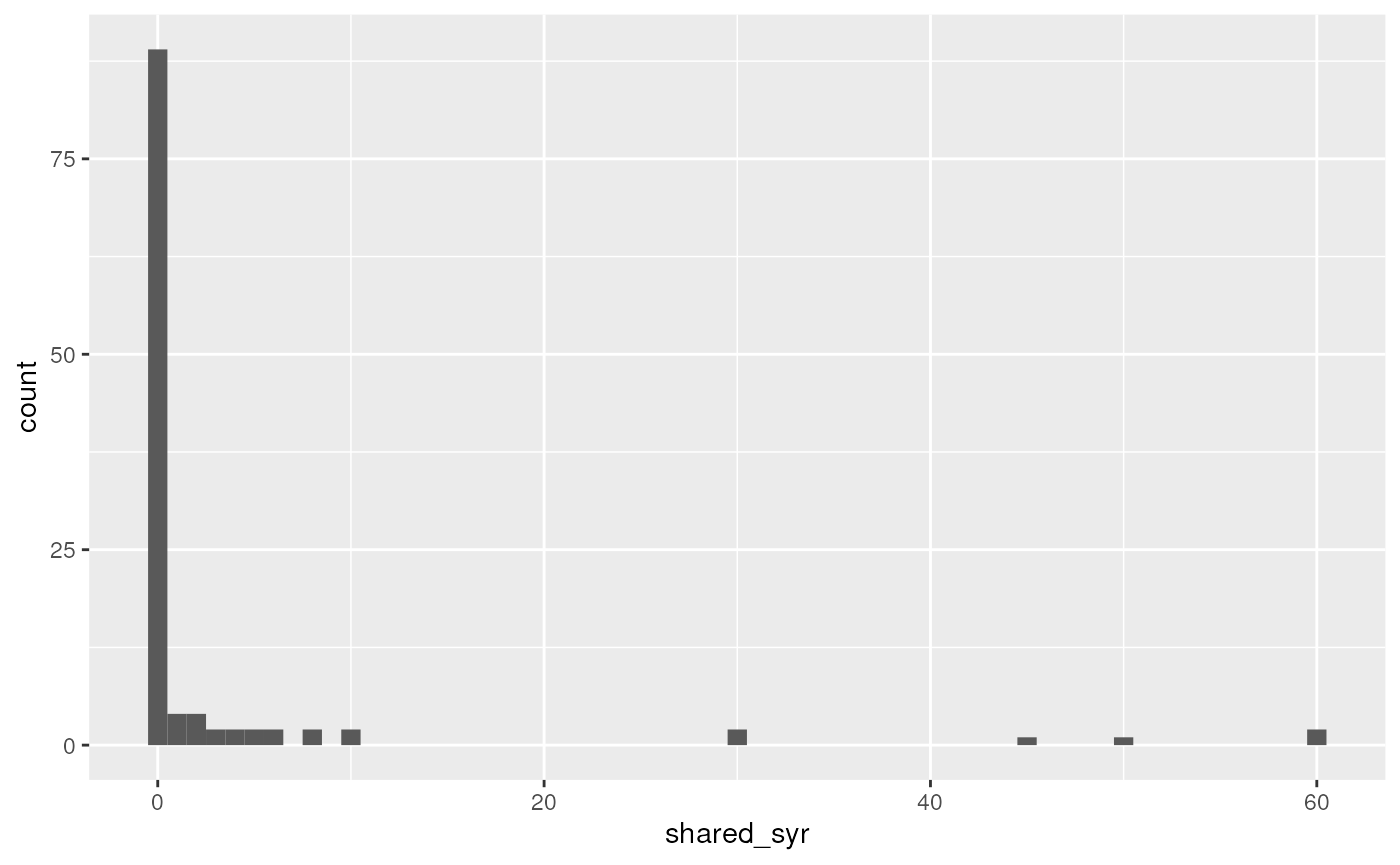

Fit Poisson and Negative Binomial models as in the lecture, with and without zero inflation.

Poisson

fit.pois <- glm(shared_syr ~ sex + ethn + homeless,
                data = needledat2,
                family = poisson(link = "log"))

Negative Binomial

library(MASS)

## 
## Attaching package: 'MASS'

## The following object is masked from 'package:dplyr':
## 
##     select

fit.negbin <- glm.nb(shared_syr ~ sex + ethn + homeless,
                data = needledat2)

Zero-inflated Poisson

The |1 creates an intercept-only zero inflation model. Substitute it with a variable name to add that variable to the count model, and use regular model formula syntax to create any zero-inflation logistic regression model you want. Or omit the | for a full zero-inflation model.

library(pscl)

## Classes and Methods for R developed in the
## Political Science Computational Laboratory
## Department of Political Science
## Stanford University
## Simon Jackman
## hurdle and zeroinfl functions by Achim Zeileis

fit.ZIpoisfull <- zeroinfl(shared_syr ~ sex + ethn + homeless,
                data = needledat2,
                dist = "poisson")

Intercept-only ZI Poisson model

fit.ZIpois <- zeroinfl(shared_syr ~ sex + ethn + homeless | 1,
                data = needledat2,
                dist = "poisson")

Intercept-only ZI Negative Binomial model

fit.ZInegbin <- zeroinfl(shared_syr ~ sex + ethn + homeless | 1,
                data = needledat2,
                dist = "negbin")

ggplot(needledat2, aes(x = ethn, y = shared_syr)) +
  geom_boxplot(varwidth = TRUE)

## Warning: Removed 2 rows containing non-finite values (`stat_boxplot()`).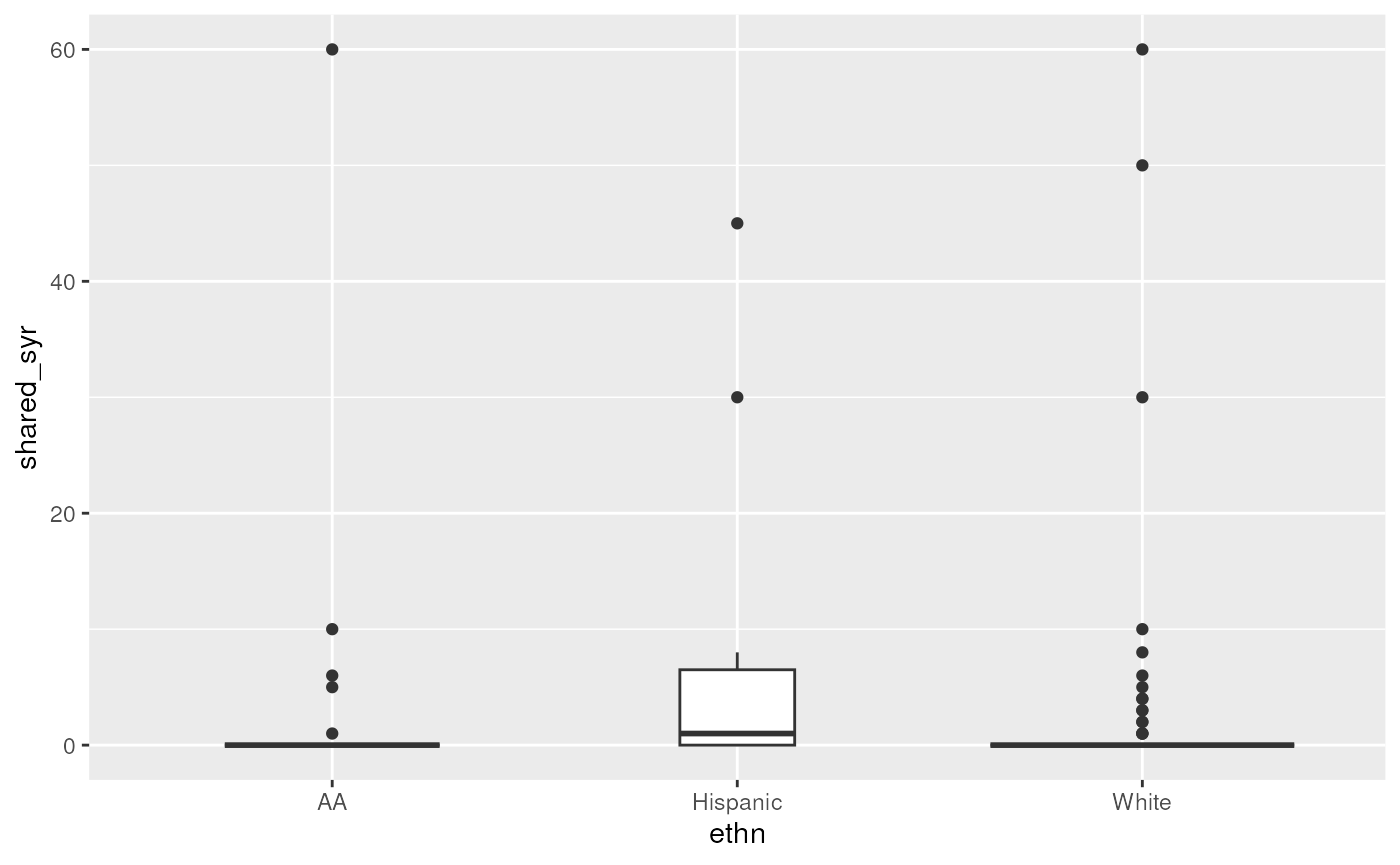

Assess whether there may be multicollinearity among the predictors

This uses model.matrix as a trick to produce a numeric matrix containing numeric and dummy variables, that can be used for calculating correlations and plotting heatmaps or dendrograms. First, assessing only three variables. Note, the first column of mm is the intercept, which must be removed.

mm <- model.matrix(~ sex + ethn + homeless, data = needledat2)
plot(hclust(as.dist(1 - cor(mm[, -1]))))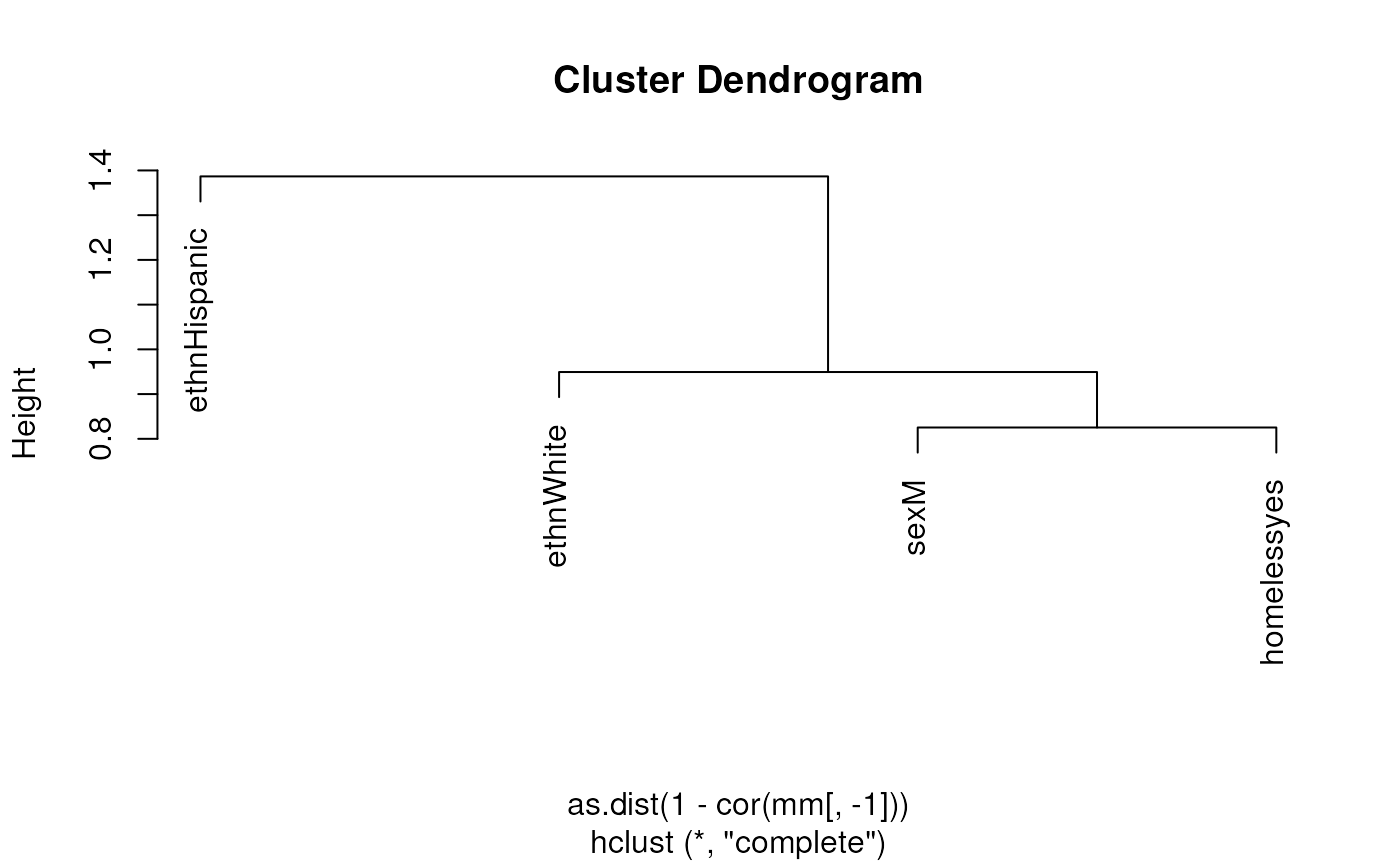

Now embed the dendrogram in a heatmap, which may be more or less informative, but worth trying. Here I use Euclidian distance for rows (patients) because some rows have zero variance and produce an error when attempting to calculate correlation, but use Pearson correlation for columns. The choice of distance metric makes this clustering look very different. See ?pheatmap for other distance metric options. There are also other heatmap packages, but ?pheatmap makes it easy to produce a basic heatmap.

library(pheatmap)
pheatmap(mm[, -1],
         clustering_distance_cols = "correlation",
         clustering_distance_rows = "euclidean")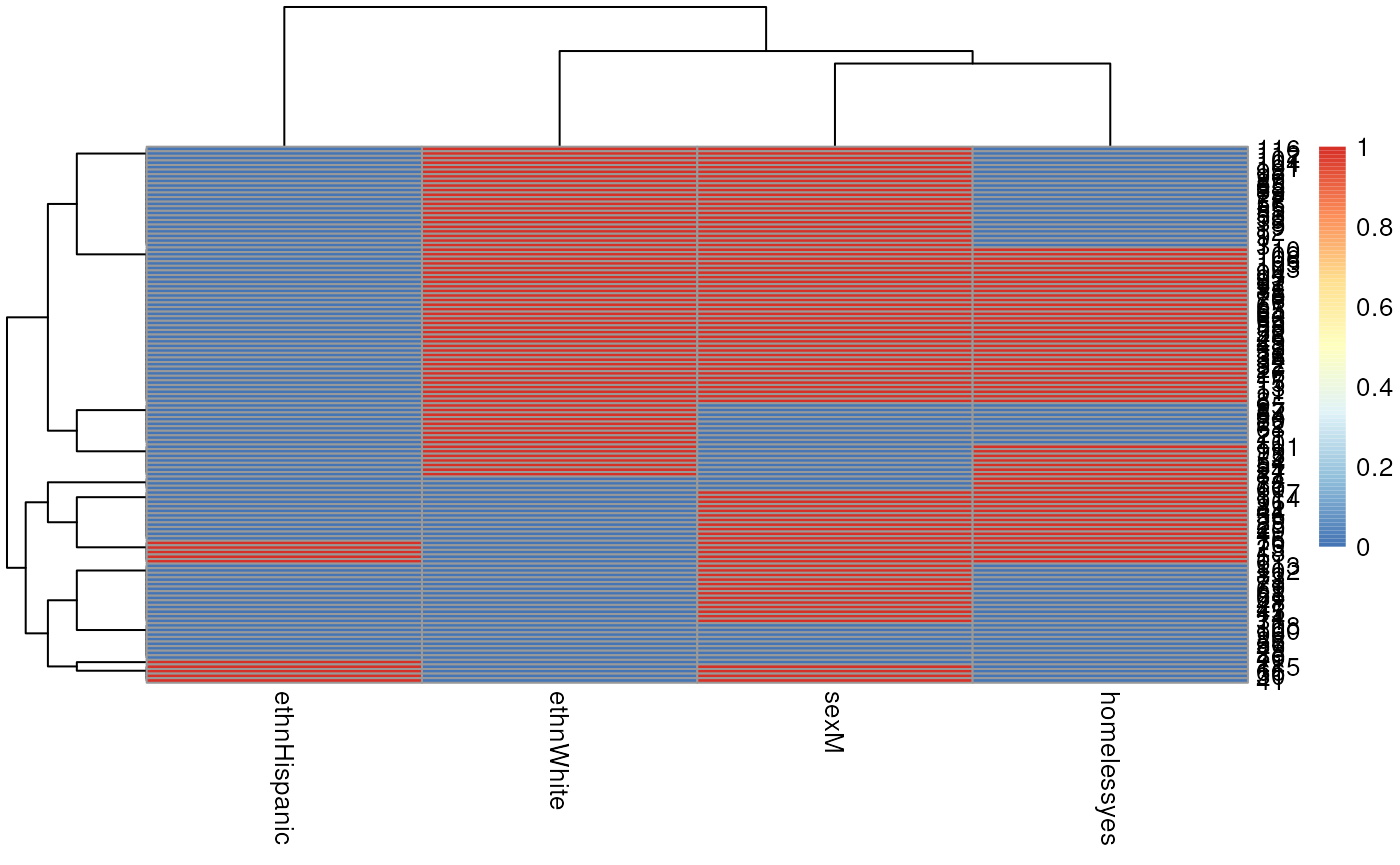

Now repeat but assessing all variables, removing id because it’s just an identifier, and shsyryn because it has zero variance.

mm <- model.matrix(~ . - id - shsyryn, data = needledat2)[, -1] #[, -1] gets rid of intercept
plot(hclust(as.dist(1 - cor(mm))))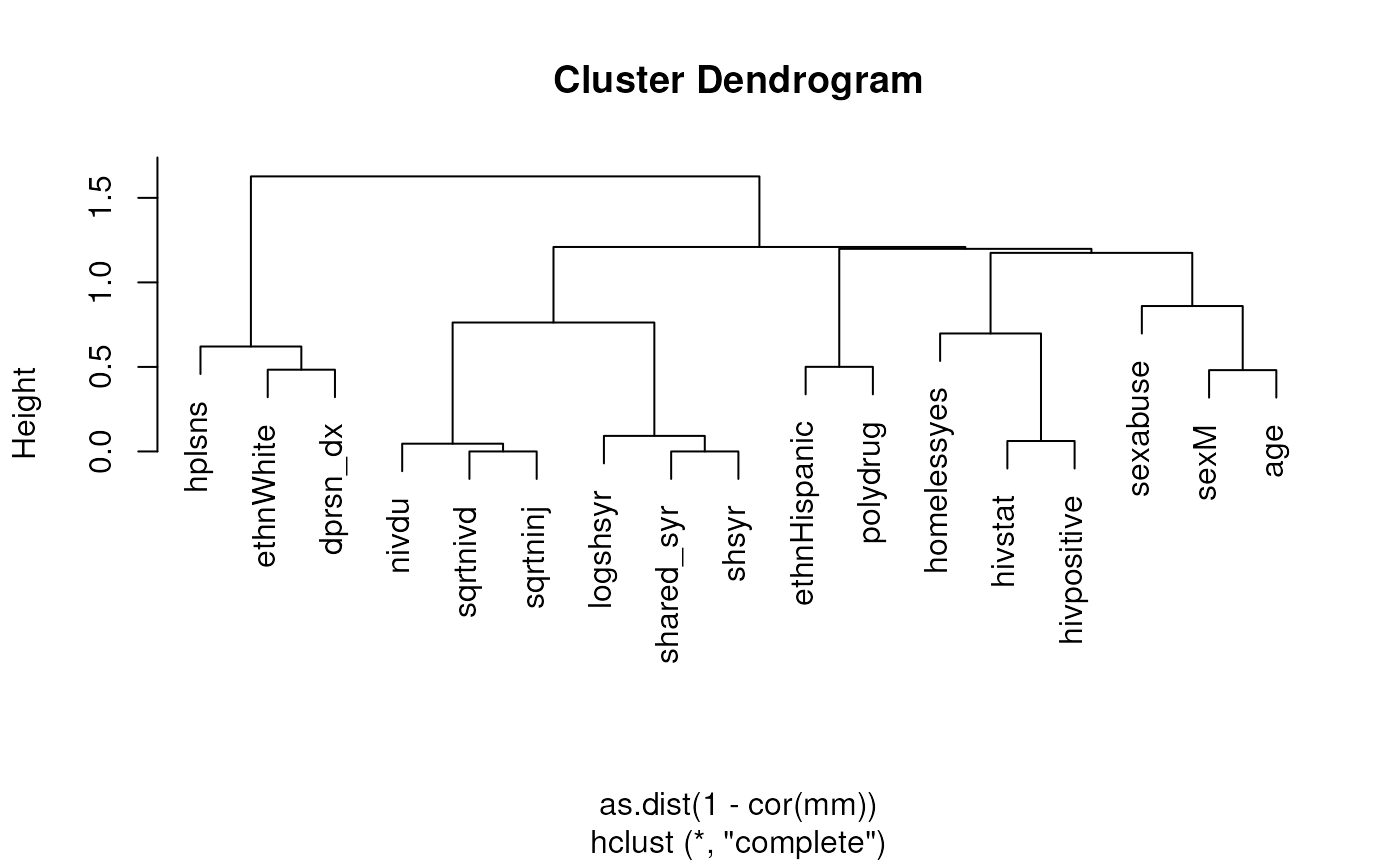

library(pheatmap)
pheatmap(mm,
         clustering_distance_cols = "correlation",
         clustering_distance_rows = "correlation")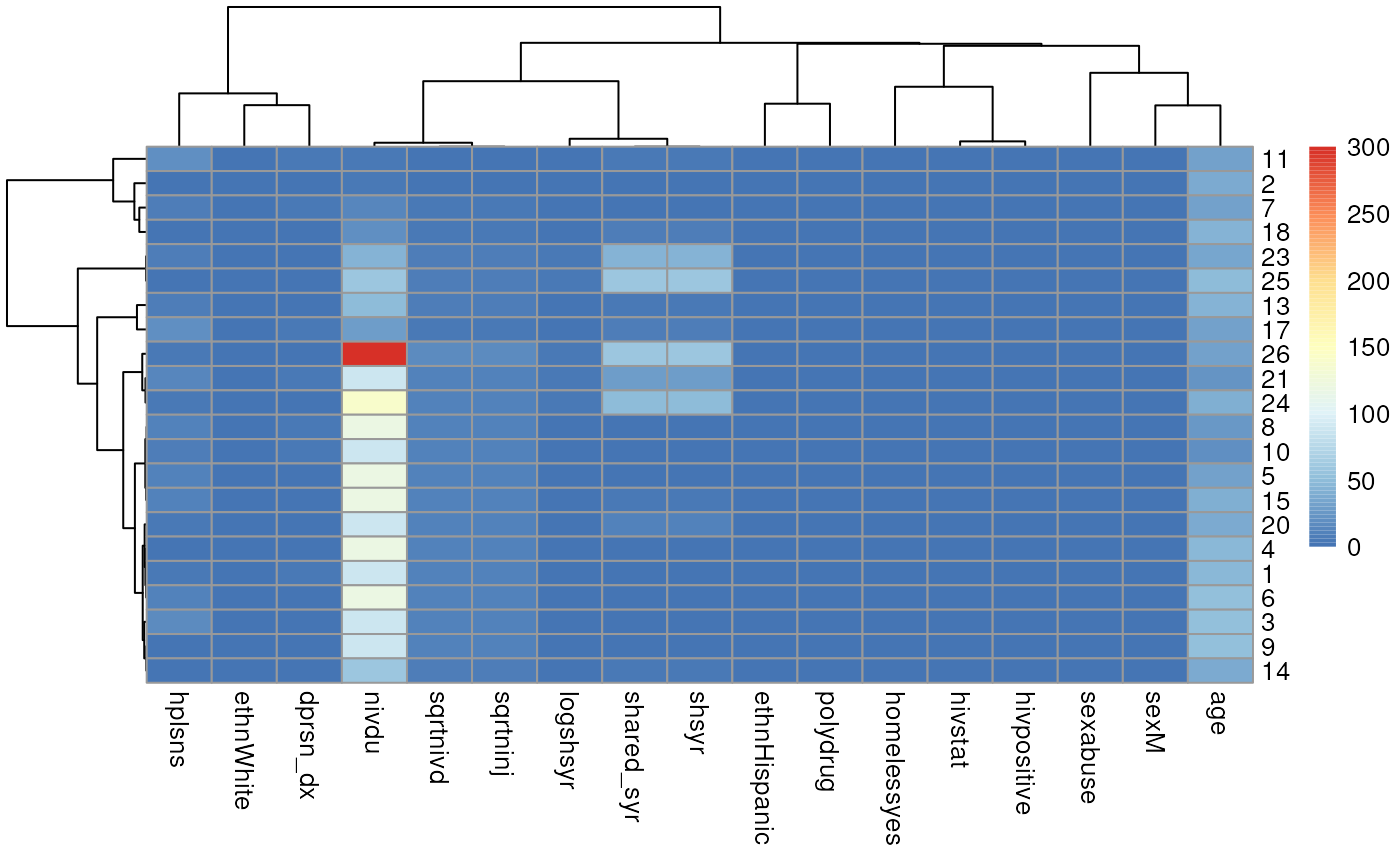

Use chi-square nested deviance tests to assess which model seems to fit best.

I want to calculate the log-likelihood from each model. The simplest way is to call the logLik function one at a time:

logLik(fit.pois)

## 'log Lik.' -730.0133 (df=5)

logLik(fit.negbin)

## 'log Lik.' -147.1277 (df=6)

logLik(fit.ZIpois)

## 'log Lik.' -303.0276 (df=6)

logLik(fit.ZInegbin)

## 'log Lik.' -146.7677 (df=7)

Just to demonstrate a fancier way that could be used on many models, I’ll create a list of model objects:

listoffits <-
  list(
    pois = fit.pois,
    negbin = fit.negbin,
    ZIpois = fit.ZIpois,
    ZInegbin = fit.ZInegbin
  )

Then demonstrate how the lapply (also related functions like sapply) can be used to implicitly loop over elements of a list, to do exactly the same thing:

lapply(listoffits, logLik)

## $pois
## 'log Lik.' -730.0133 (df=5)
## 
## $negbin
## 'log Lik.' -147.1277 (df=6)
## 
## $ZIpois
## 'log Lik.' -303.0276 (df=6)
## 
## $ZInegbin
## 'log Lik.' -146.7677 (df=7)

OK now to actually answer the question. Just to get an idea of how big a difference in \(-2 \times log(likelihood)\) would be statistically significant on one difference of degrees of freedom:

qchisq(0.95, df = 1)

## [1] 3.841459

Or two degrees of freedom:

qchisq(0.95, df = 2)

## [1] 5.991465

All the differences in double log-likelihoods above are much larger (in the hundreds) than these critical significance values, except for the difference between Negative Binomial and zero-inflated negative binomial models. So it doesn’t look like zero inflation helped the Negative Binomial distribution model, but it helped the Poisson model, and the Negative Binomial model fits better than the Poisson model.

Create residual deviance plots using the functions defined in the lecture.

These were the (base graphics) functions defined to create the first two panels of residuals plots for all of these types of models.

plotpanel1 <- function(fit, ...) {
  plot(
    x = predict(fit),
    y = residuals(fit, type = "pearson"),
    xlab = "Predicted Values",
    ylab = "Pearson Residuals",
    ...
  )
  abline(h = 0, lty = 3)
  lines(lowess(x = predict(fit), y = resid(fit, type = "pearson")),
        col = "red")
}
plotpanel2 <- function(fit, ...) {
  resids <- scale(residuals(fit, type = "pearson"))
  qqnorm(resids, ylab = "Std Pearson resid.", ...)
  qqline(resids)
}

Let’s make these plots. As a shortcut, remember that list of models? I’m going to use an explicit for loop this time instead of lapply so that I can use the vector names as plot titles.

Although we saw some evidence from the chi-square test that the Negative Binomial distribution fit better than the Poisson distribution (not surprising since these data are very over-dispersed), these diagnostic plots show the Negative Binomial distribution still does not fit well at all. I would take any interpretation of the coefficients of these models with plenty of skepticism. But this dataset is tricky and I’m not sure offhand of a good model to fit it.

Note, the line par(mfrow=c(1, 2)) only works for base graphics (not ggplot2), and creates a 1 row by 2 column plot panel.

par(mfrow=c(1, 2))
for (i in seq_along(listoffits)){
  plotpanel1(listoffits[[i]], main = names(listoffits)[i])
  plotpanel2(listoffits[[i]], main = names(listoffits)[i])
}

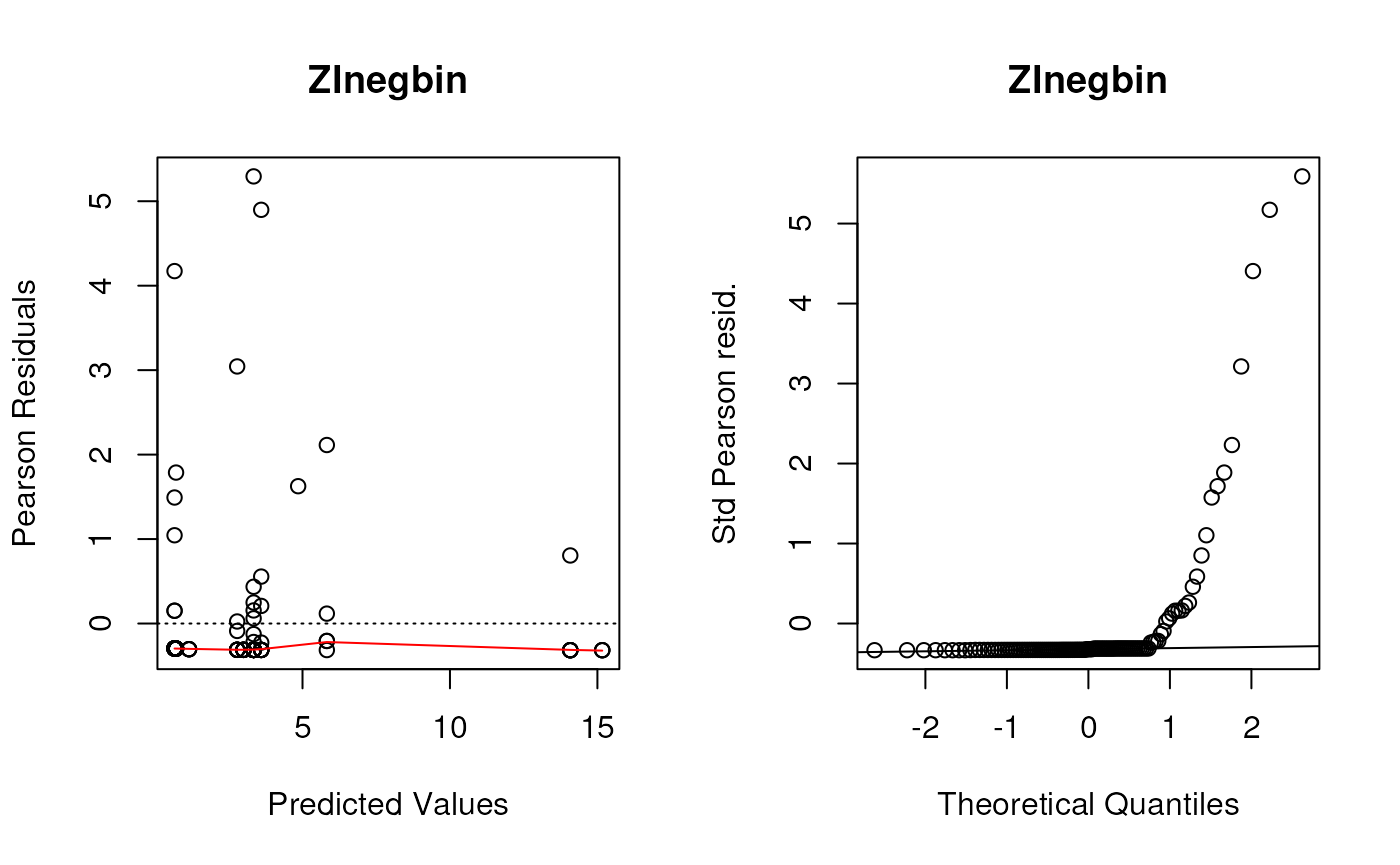
Plot predicted and observed counts

Here is a data.frame that we can use to make histograms, density plots, etc.

preds <- data.frame(observed = fit.pois$y,
                    poisson = predict(fit.pois),
                    negbin = predict(fit.negbin),
                    ZIpois = predict(fit.ZIpois),
                    ZInegbin = predict(fit.ZInegbin))

Just to help with pivoting, let’s pivot this into long-format:

preds.long <- pivot_longer(preds, everything())

What did this do?

summary(preds.long)

##      name               value        
##  Length:575         Min.   :-0.5506  
##  Class :character   1st Qu.: 0.0000  
##  Mode  :character   Median : 1.1446  
##                     Mean   : 2.3125  
##                     3rd Qu.: 2.5691  
##                     Max.   :60.0000

Boxplot

ggplot(preds.long, aes(x = name, y = value)) + geom_boxplot()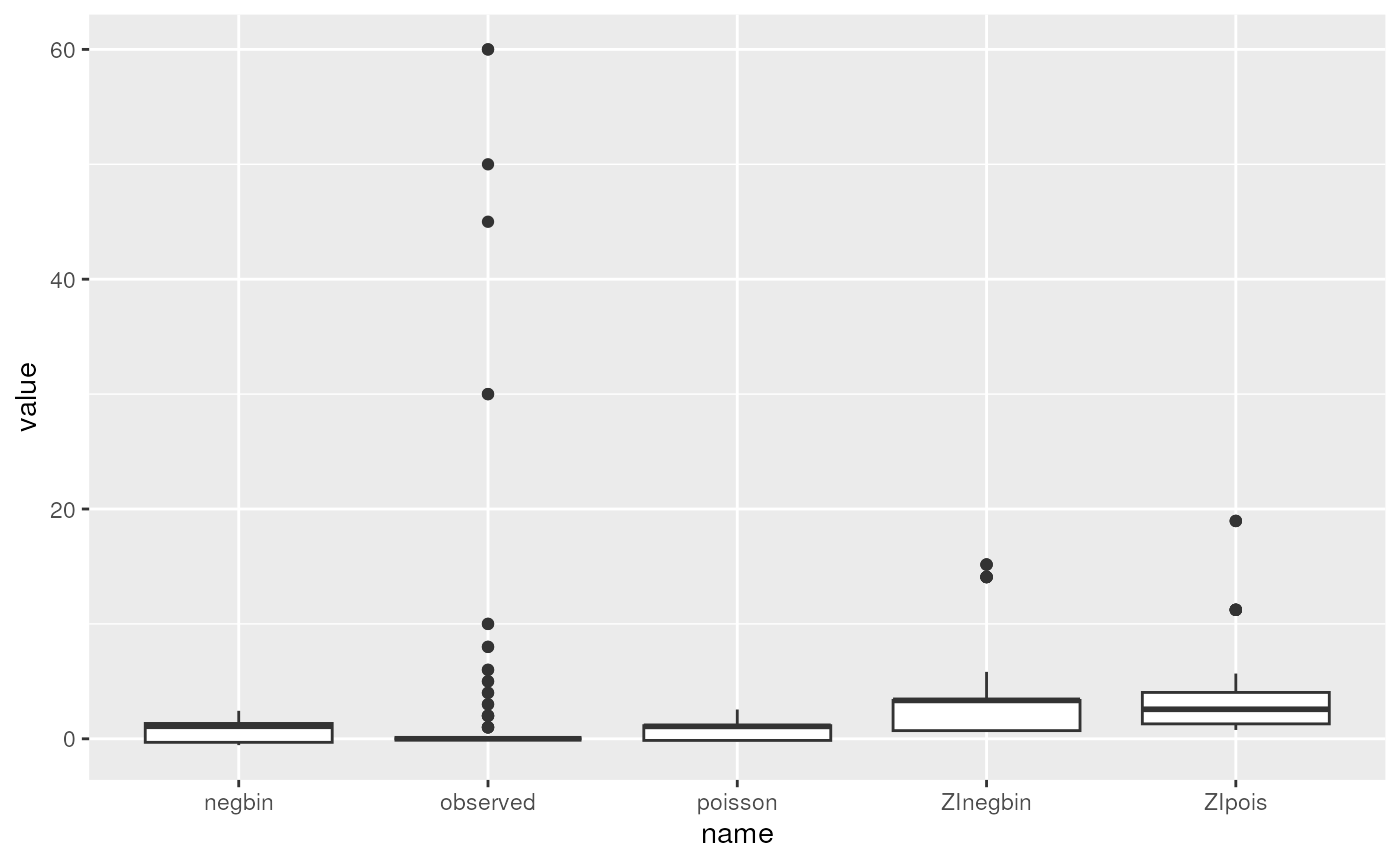

Histogram with facet_wrap

ggplot(preds.long, aes(x = value)) + 
  facet_wrap(~name) +
  geom_histogram(binwidth = 1)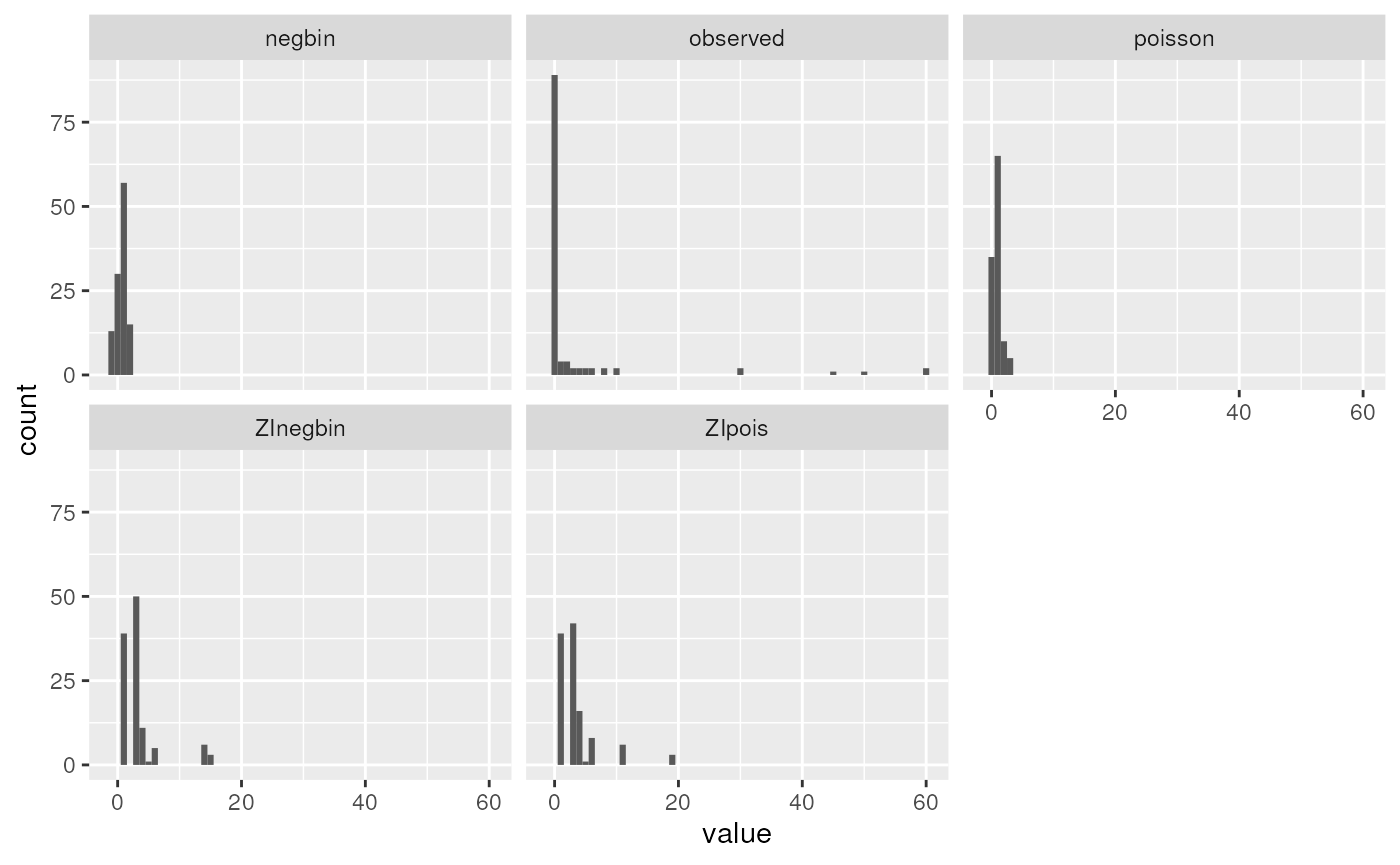

We can see that none of the models come close to modeling the extreme observed counts of 30+. In reality, these might require a more complex mixture model: for example a mixture of zero-inflation plus two different count distributions, one with a much higher mean. This is beyond the scope of the course, but it is possible to fit more complex mixture models that could fit this dataset better.

Levi Waldron