Session 7: Survival Analysis 2

Levi Waldron

Learning objectives and outline

Learning objectives

1. Define proportional hazards
2. Perform and interpret Cox proportional hazards regression
3. Define time-dependent covariates and their use
4. Identify the differences between parametric and semi-parametric survival models
5. Identify situations when a parametric survival model might be useful

Outline

1. Review of survival and hazard functions
2. The Cox proportional hazards model
   • interpretation and inference
   • what are proportional hazards
   • when hazards aren’t proportional
3. Parametric vs semi-parametric survival models

• Vittinghoff sections 6.1-6.2, 6.4

Review of survival and hazard functions

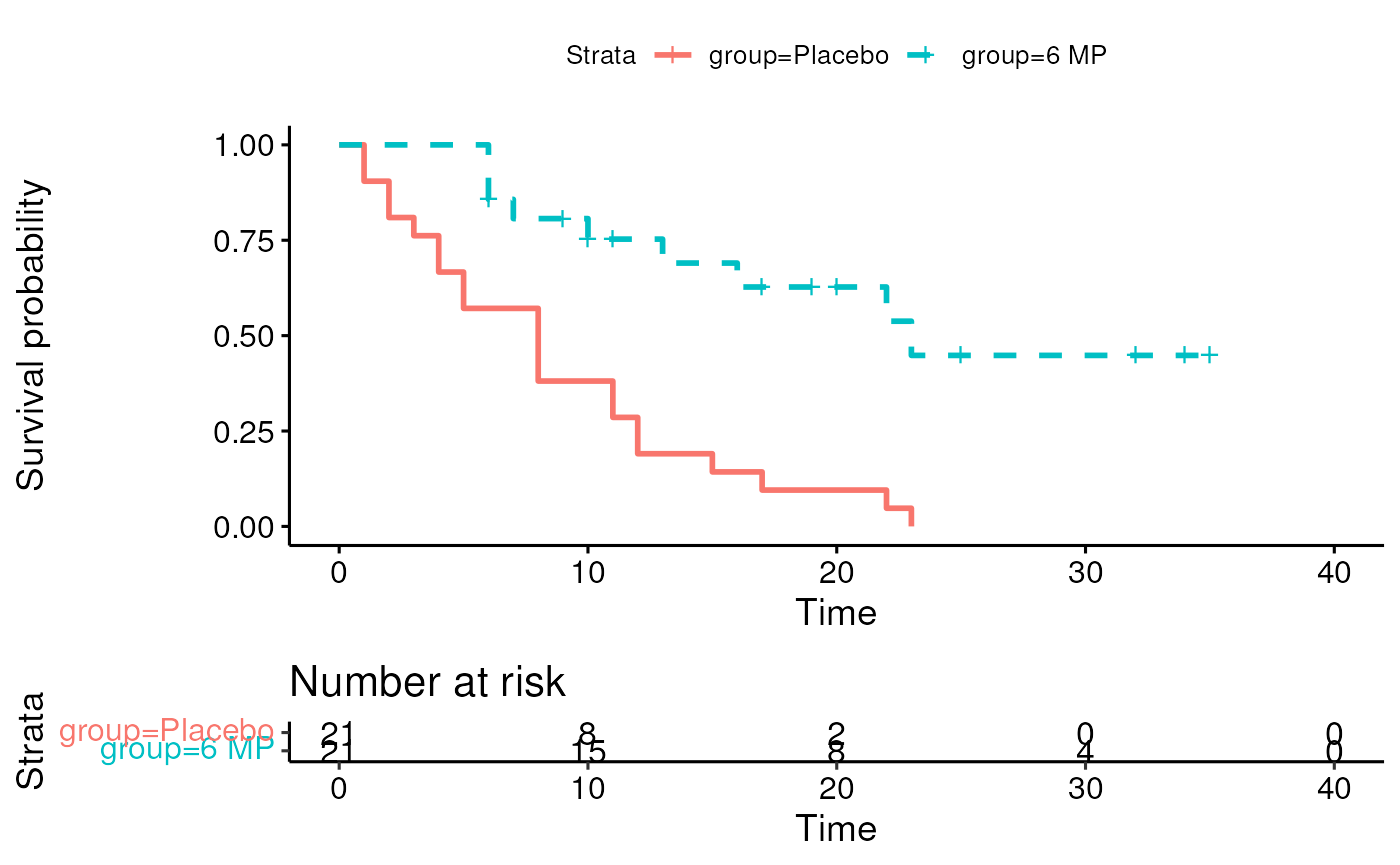
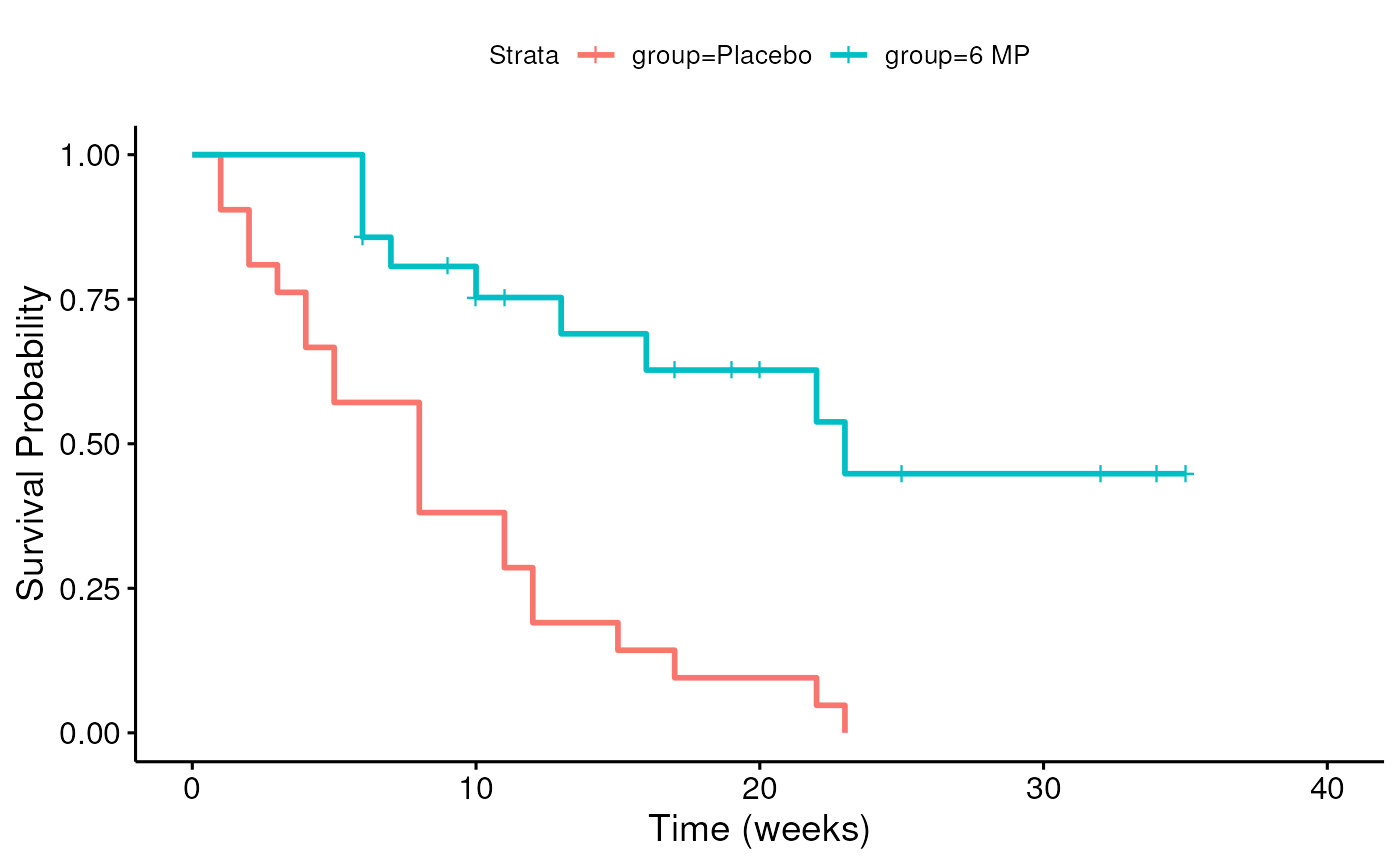
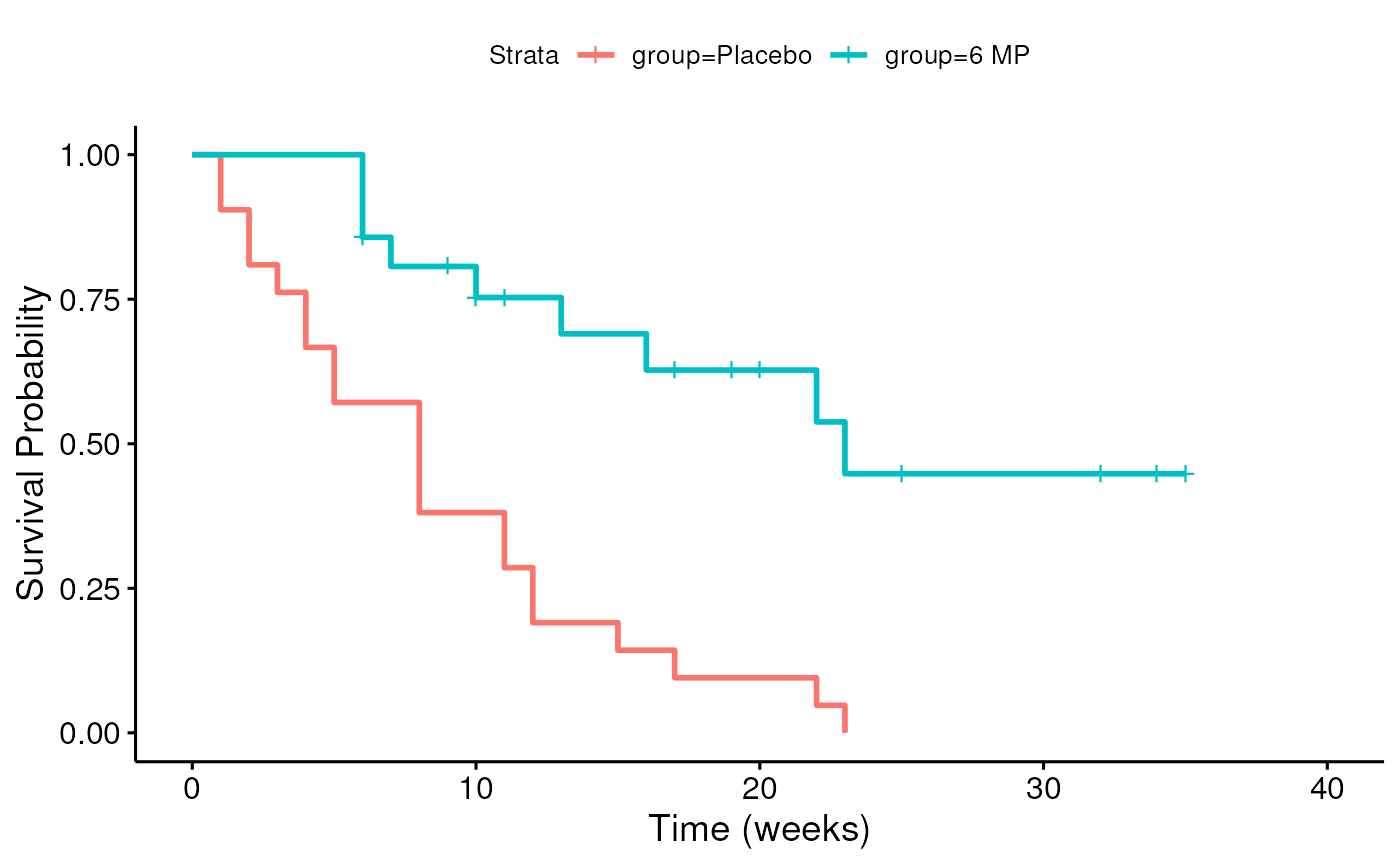
Recall leukemia Example

• Study of 6-mercaptopurine (6-MP) maintenance therapy for children in remission from acute lymphoblastic leukemia (ALL)
• 42 patients achieved remission from induction therapy and were then randomized in equal numbers to 6-MP or placebo.
• Survival time studied was from randomization until relapse.

Leukemia follow-up table

leukemia Follow-up Table

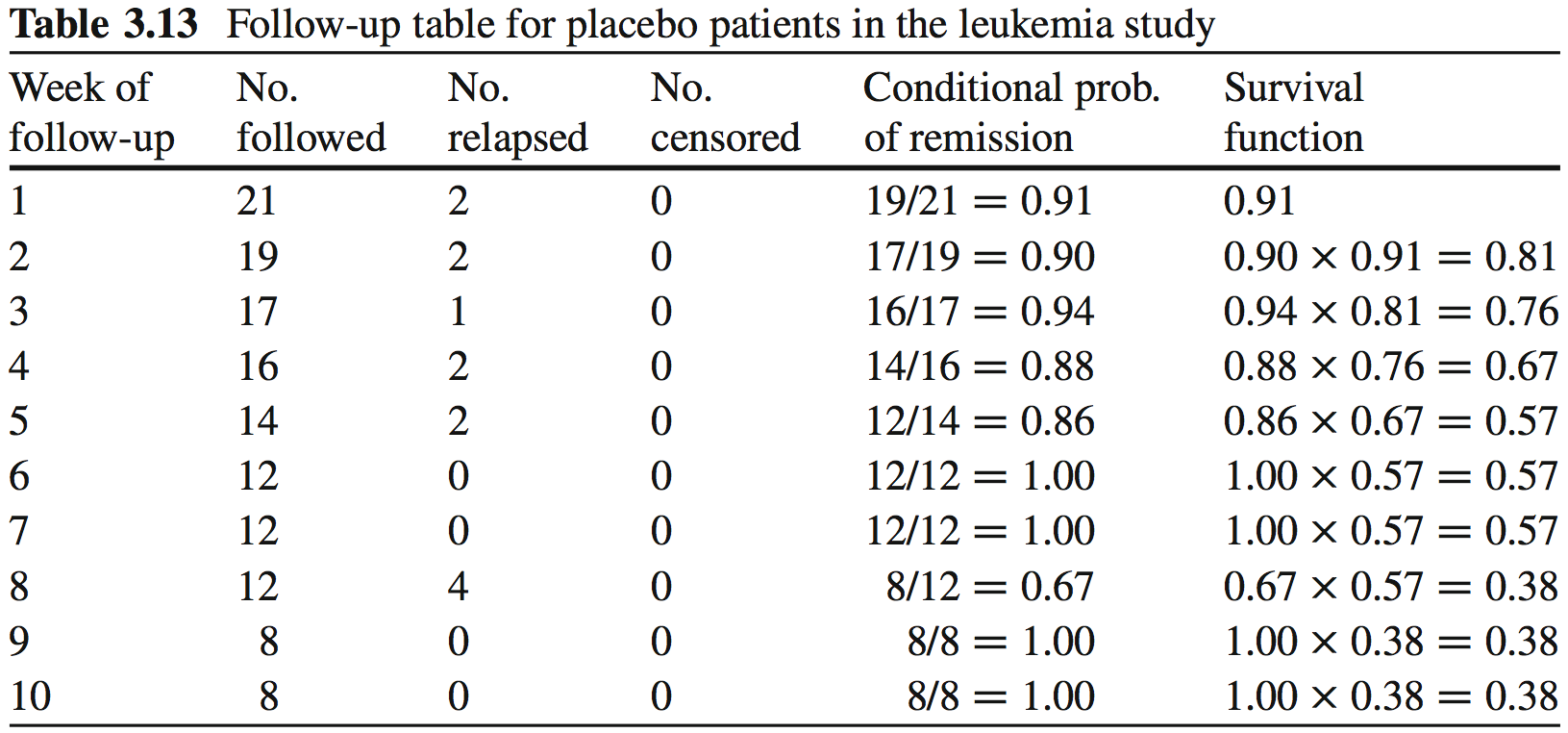
This is the Kaplan-Meier Estimate $\hat S(t)$ of the Survival function $S(t)$.

Leukemia Kaplan-Meier plot

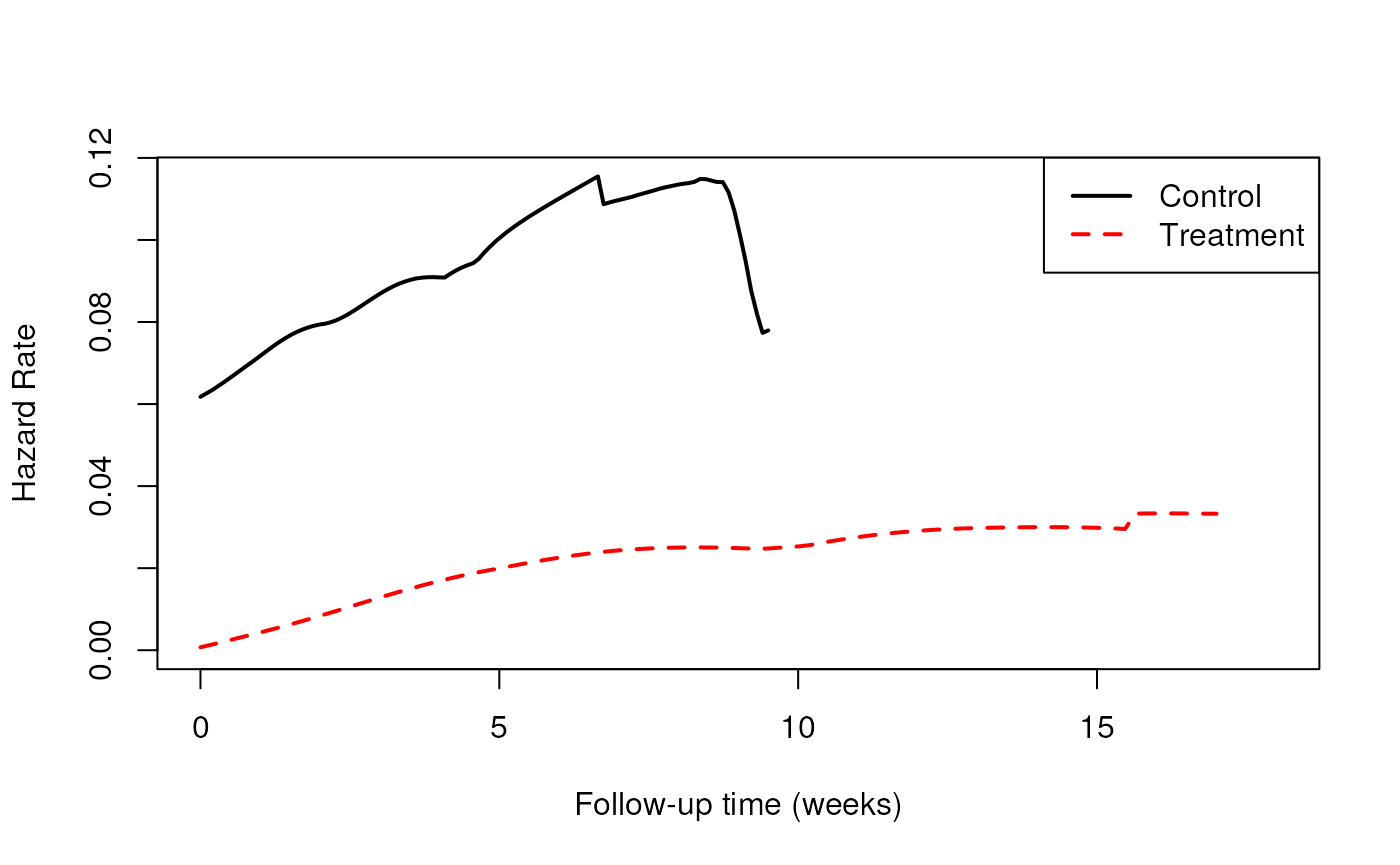
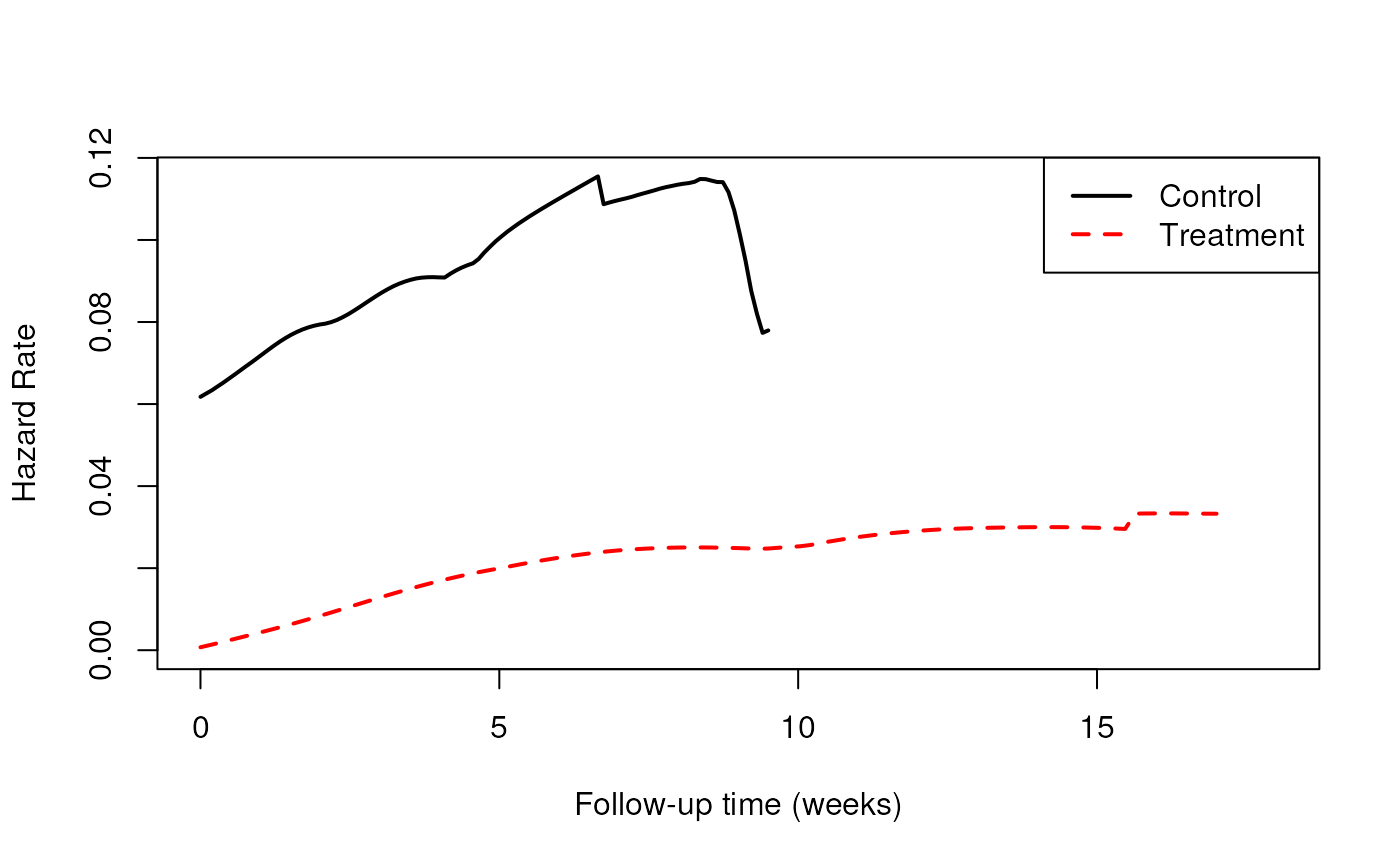
The hazard function h(t)

• Definition: The survival function at time t, denoted $S(t)$, is the probability of being event-free at t. Equivalently, it is the probability that the survival time is greater than t.

• Definition: The cumulative event function at time t, denoted $F(t)$, is the probability that the event has occurred by time t, or equivalently, the probability that the survival time is less than or equal to t. $F(t) = 1-S(t)$.

• Definition: The hazard function $h(t)$ is the short-term event rate for subjects who have not yet experienced an event.

  • $h(t)$ is the probability of an event in the time interval $[t, t+s]$ (s is small), given that the individual has survived up to time t $$h(t) = \lim_{s \to 0} \frac{Pr(t \leq T < t+s | T \ge t)}{s}$$

Leukemia dataset $S(t)$

Survival function $S(t)$

Leukemia dataset $h(t)$

Hazard function $h(t)$

SAS and R Source code

The Hazard Ratio (HR)

• If we are comparing the hazards of a control and a treatment group, it could in general be a function of time:
  • $HR(t) = h_T(t) / h_C(t)$
• Interpretation: the risk of event for the treatment group compared to the control group, as a function of time

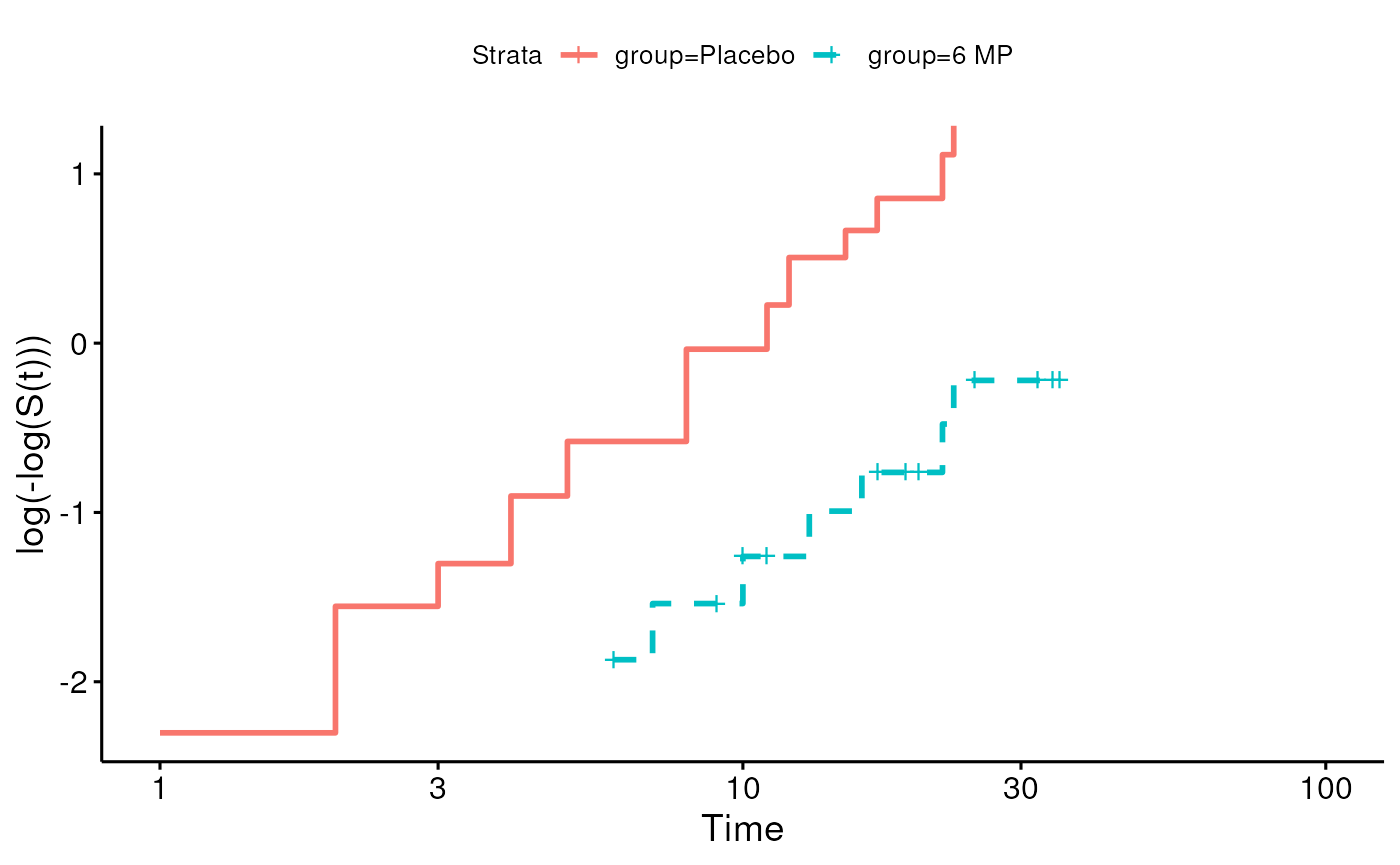
The Proportional Hazards Assumption

• Definition: Under the proportional hazards assumption, the hazard ratio does not vary with time. That is, $HR(t) \equiv HR$.

• In other words, $HR$ does not vary with time

  • $HR(t)$ is a constant, $HR$, at all times t
  • this assumption is about the population, of course there will be sampling variation

A nice proportional hazards dataset

Vittinghoff Figure 6.3, p. 210

The hazard function h(t) (leukemia dataset)

## # A tibble: 2 × 2
##   group   haz    
##   <fct>   <list> 
## 1 Placebo <muhaz>
## 2 6 MP    <muhaz>

Log-minus-log plot

Recall previous regression models

$$E[y_i|x_i] = \beta_1 x_{1i} + \beta_2 x_{2i} + ... + \beta_p x_{pi}$$

• $x_p$ are the predictors or independent variables
• $y$ is the outcome, response, or dependent variable
• $E[y|x]$ is the expected value of $y$ given $x$
• $\beta_p$ are the regression coefficients

For logistic regression: $$Logit(P(x_i)) = log \left( \frac{P(x_i)}{1-P(x_i)} \right) = \beta_1 x_{1i} + \beta_2 x_{2i} + ... + \beta_p x_{pi}$$

For log-linear regression: $$log(E[y_i|x_i]) = \beta_1 x_{1i} + \beta_2 x_{2i} + ... + \beta_p x_{pi}$$

Cox proportional hazards model

Cox proportional hazards model

• Cox proportional hazards regression assesses relationship between a right-censored, time-to-event outcome and predictors:
  • categorical variables (e.g., treatment groups)
  • continuous variables $$log(HR(x_i)) = log \frac{h(t|x_i)}{h_0(t)} = \beta_1 x_{1i} + \beta_2 x_{2i} + ... + \beta_p x_{pi}$$
• $HR(x_i)$ is the hazard of patient $i$ relative to baseline
• $h(t|x_i)$ is the time-dependent hazard function $h(t)$ for patient $i$
• $h_0(t)$ is the baseline hazard function

Multiplicative or additive model?

Interpretation of coefficients

• Coefficients $\beta$ for a categorical / binary predictor:
  • $\beta$ is the $log$ of the ratio of hazards for the comparison group relative to reference group ($log(HR)$)
• Coefficients $\beta$ for a continuous predictor:
  • $\beta$ is the $log$ of the ratio of hazards for someone having a one unit higher value of $x$ (1 year, 1mm Hg, etc)
• If the hazard ratio ($exp(\beta)$) is close to 1 then the predictor does not affect survival
• If the hazard ratio is less than 1 then the predictor is protective (associated with improved survival)
• If the hazard ratio is greater than 1 then the predictor is associated with increased risk (= decreased survival)

Hypothesis testing and CIs

• Wald Test or Likelihood Ratio Test for coefficients
  • $H_0: \beta=0, H_a: \beta \neq 0$
  • equivalent to $H_0: HR=1, H_a: HR \neq 1$
• CIs typically obtained from Wald Test, reported for $HR$

Cox PH regression for Leukemia dataset

## Call:
## coxph(formula = Surv(time, cens) ~ group, data = leuk)
## 
##   n= 42, number of events= 30 
## 
##              coef exp(coef) se(coef)      z Pr(>|z|)    
## group6 MP -1.5721    0.2076   0.4124 -3.812 0.000138 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##           exp(coef) exp(-coef) lower .95 upper .95
## group6 MP    0.2076      4.817   0.09251    0.4659
## 
## Concordance= 0.69  (se = 0.041 )
## Likelihood ratio test= 16.35  on 1 df,   p=5e-05
## Wald test            = 14.53  on 1 df,   p=1e-04
## Score (logrank) test = 17.25  on 1 df,   p=3e-05

Cox PH is a semi-parametric model

• Cox proportional hazards model is semi-parametric:
  • assumes proportional hazards (PH), but no assumption on $h_0(t)$
  • robust if PH assumption is not violated
  • time-dependent covariates may resolve apparent violations of the PH assumption.

Summary: proportional hazards assumption

• Constant hazard ratio between groups over time (proportional hazards)
• A linear association between the natural log of the relative hazard and the predictors (log-linearity)
  • A multiplicative relationship between the predictors and the hazard
• Uninformative censoring

What to do when proportional hazards doesn’t hold?

• Time-dependent covariates
• Definition: A time-dependent covariate is a predictor whose values may vary with time.
• Basic rule: You cannot look into the future in your analysis (even though it took place in the past) E.g.:
  • breast cancer chemotherapy patients divided into groups based on how much of the planned dose they received
  • patients divided into groups based on early response to treatment (shrinkage of tumor, lowering of cholesterol, etc)
  • interpolation of the values of a laboratory test linearly between observation times
  • removing subjects who do not finish the treatment plan
  • imputing the date of an adverse event as midway between observation times

Source: Using Time Dependent Covariates and Time Dependent Coefficients in the Cox Model

Immortal time bias example

• Immortal time bias is an example of looking into the future.
• E.g. Yee et al. reported that new statin users reported a 26% reduction in the risk of diabetes progression with one year or more of treatment relative to never-users (adjusted HR 0.74, 95% CI: 0.56 to 0.97).
  • New users excludes those who had received a lipid lowering drug from three years before to six months after cohort entry
• HR>1 was expected:people whose diabetes progresses are more likely to develop cardiovascular disease, an indication for statins.
• This is a result of an analysis error. Why?

• Yee et al. Statin use in type 2 diabetes mellitus is associated with a delay in starting insulin (http://onlinelibrary.wiley.com/doi/10.1111/j.1464-5491.2004.01263.x/full)

Immortal time bias example (cont’d)

• What was the analysis error?
  • “new statin user” group was defined based on future initiation: knowledge unknown at the time of entry into the study
  • guaranteed no events for statin users from cohort entry to start of statin use
  • thus all persons in the treated group are “immortal” from time 0 until the initiation of statin treatment
  • this period of immortality made treatment look more effective

Parametric survival models

What are “parametric” survival models?

• “Parametric” models estimate additional parameters for the baseline hazard, e.g.:
  • Weibull: hazard function is a polynomial
  • exponential: hazard function is constant over time, survival function is exponential (special case of Weibull): e.g. healthy population with randomly occurring events
  • many other options for assumption of distributions
• In most common implementation a log-transform of the time variable is used
  • then can be interpreted as Accelerated Failure Time (AFT) models.

Coefficients in parametric models

• The interpretation of $\beta$ coefficients is different:
  • Cox model: $log(HR)$
  • AFT models: $log(survival time ratio)$
  • The sign is opposite (i.e. if one is positive the other is negative)

Why use a parametric survival model?

• Can be more powerful if assumption is correct
  • may help with small numbers of events
• Extra capabilities:
  • smooth estimation of baseline hazard
  • extrapolation
  • complicated censoring
• Easy to interpret: coefficients are $log(survival time ratio)$
• Easy to fit: replace survival::coxph with survival::survreg

Why not to use a parametric survival model?

• Depend on correct specification of baseline hazard model
• Even if correctly specified, may not provide much improvement in efficiency
• Still make a proportionality assumption, on survival functions