Session 2: Linear and logistic regression as Generalized Linear Models

Levi Waldron

Learning Objectives and Outline

Learning objectives

1. define generalized linear models (GLM)
2. define linear and logistic regression as special cases of GLMs
3. distinguish between additive and multiplicative models
4. define Pearson and deviance residuals
5. describe application of the Wald test

Outline

1. Brief overview of multiple regression (Vittinghoff 4.1-4.3)
2. Linear Regression as a GLM (Vittinghoff 4.1-4.3)
3. Logistic Regression as a GLM (Vittinghoff 5.1-5.3)
4. Statistical inference for logistic regression (Vittinghoff 5.1-5.3)

Review of multiple linear regression

Systematic component

$$E[y|x] = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_p x_p$$

• $x_p$ are the predictors or independent variables
• $y$ is the outcome, response, or dependent variable
• $E[y|x]$ is the expected value of $y$ given $x$
• $\beta_p$ are the regression coefficients

Systematic plus random component

$y_i = E[y|x] + \epsilon_i$

$y_i = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_p x_p + \epsilon_i$

Assumption: $\epsilon_i \stackrel{iid}{\sim} N(0, \sigma_\epsilon^2)$

• Normal distribution
• Mean zero at every value of predictors
• Constant variance at every value of predictors
• Values that are statistically independent

Linear Regression as a GLM

Generalized Linear Models (GLM)

• Linear regression is a special case of a broad family of models called “Generalized Linear Models” (GLM)
• This unifying approach allows to fit a large set of models using maximum likelihood estimation methods (MLE) (Nelder & Wedderburn, 1972)
• Can model many types of data directly using appropriate distributions, e.g. Poisson distribution for count data
• Transformations of $Y$ not needed

Components of GLM

• Random component specifies the conditional distribution for the response variable
  • doesn’t have to be normal
  • can be any distribution in the “exponential” family of distributions
• Systematic component specifies linear function of predictors (linear predictor)
• Link [denoted by g(.)] specifies the relationship between the expected value of the random component and the systematic component
  • can be linear or nonlinear

Linear Regression as GLM

• The model: $y_i = E[y|x] + \epsilon_i = \beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + ... + \beta_p x_{pi} + \epsilon_i$

• Random component of $y_i$ is normally distributed: $\epsilon_i \stackrel{iid}{\sim} N(0, \sigma_\epsilon^2)$

• Systematic component (linear predictor): $\beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + ... + \beta_p x_{pi}$

• Link function here is the identity link: $g(E(y | x)) = E(y | x)$. We are modeling the mean directly, no transformation.

Logistic Regression as a GLM

The logistic regression model

• The model: $$Logit(P(x)) = log \left( \frac{P(x)}{1-P(x)} \right) = \beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + ... + \beta_p x_{pi}$$

• Random component: $y_i$ follows a Binomial distribution (outcome is a binary variable)

• Systematic component: linear predictor $$\beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + ... + \beta_p x_{pi}$$

• Link function: logit (log of the odds that the event occurs)

$$g(P(x)) = logit(P(x)) = log\left( \frac{P(x)}{1-P(x)} \right)$$

$$P(x) = g^{-1}\left( \beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + ... + \beta_p x_{pi} \right)$$

The logit function

logit <- function(P) log(P/(1-P))
plot(logit, xlab="Probability", ylab="Log-odds",
     cex.lab=1.5, cex.axis=1.5)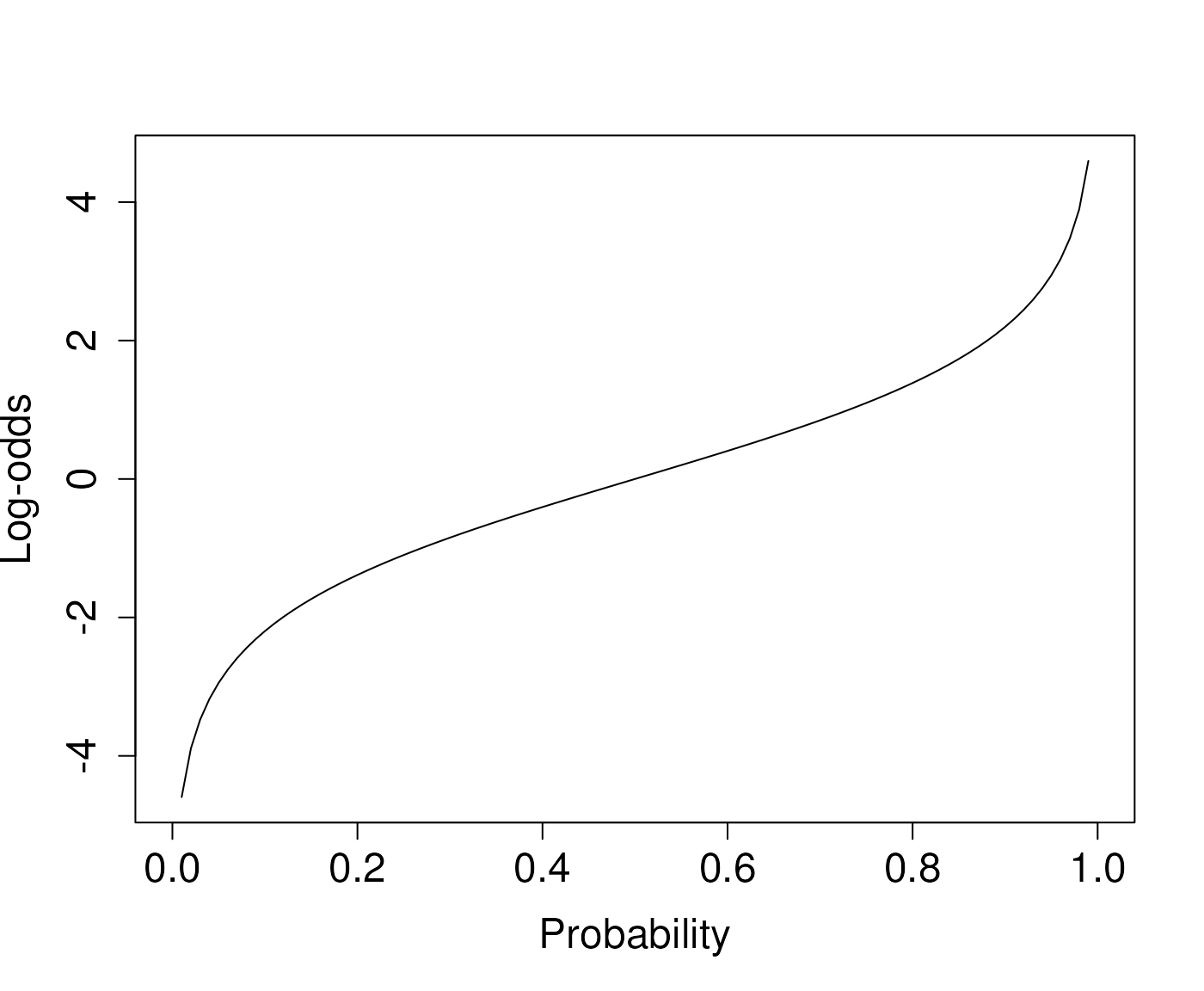

Inverse logit function

invLogit <- function(x) 1/(1+exp(-x))

Example: contraceptive use data

Age (years)	<25 (N=4)	25-29 (N=4)	30-39 (N=4)	40-49 (N=4)	Overall (N=16)
education
high	2 (50.0%)	2 (50.0%)	2 (50.0%)	2 (50.0%)	8 (50.0%)
low	2 (50.0%)	2 (50.0%)	2 (50.0%)	2 (50.0%)	8 (50.0%)
wantsMore
no	2 (50.0%)	2 (50.0%)	2 (50.0%)	2 (50.0%)	8 (50.0%)
yes	2 (50.0%)	2 (50.0%)	2 (50.0%)	2 (50.0%)	8 (50.0%)
percentusing
Mean (SD)	18.8 (7.64)	27.1 (6.53)	38.8 (15.6)	46.9 (23.8)	32.9 (17.5)
Median [Min, Max]	18.2 [10.2, 28.6]	27.6 [18.9, 34.5]	39.5 [22.8, 53.4]	50.5 [14.6, 72.1]	28.3 [10.2, 72.1]

Source: http://data.princeton.edu/wws509/datasets/#cuse. Note, this table represents rows of the source data, not number of participants. See the lab to make a table that summarizes the participants.

Perform regression

• Outcome: whether using contraceptives or not
• Predictors: age, education level (high/low), whether wants more children or not

fit1 <- glm(cbind(using, notUsing) ~ age + education + wantsMore, 
           data=cuse, family=binomial("logit"))
summary(fit1)

## 
## Call:
## glm(formula = cbind(using, notUsing) ~ age + education + wantsMore, 
##     family = binomial("logit"), data = cuse)
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept)   -0.8082     0.1590  -5.083 3.71e-07 ***
## age25-29       0.3894     0.1759   2.214  0.02681 *  
## age30-39       0.9086     0.1646   5.519 3.40e-08 ***
## age40-49       1.1892     0.2144   5.546 2.92e-08 ***
## educationlow  -0.3250     0.1240  -2.620  0.00879 ** 
## wantsMoreyes  -0.8330     0.1175  -7.091 1.33e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 165.772  on 15  degrees of freedom
## Residual deviance:  29.917  on 10  degrees of freedom
## AIC: 113.43
## 
## Number of Fisher Scoring iterations: 4

Residuals for logistic regression

Pearson residuals for logistic regression

• Traditional residuals $y_i - E[y_i|x_i]$ don’t make sense for binary $y$.
• One alternative is Pearson residuals
  • take the difference between observed and fitted values (on probability scale 0-1), and divide by the standard deviation of the observed value.
• Let $\hat y_i$ be the best-fit predicted probability for each data point, i.e. $g^{-1}(\beta_0 + \beta_1 x_{1i} + ...)$
• $y_i$ is the observed value, either 0 or 1.

$$r_i = \frac{y_i - \hat y_i}{ \sqrt{ Var(\hat y_i) }}$$

Summing the squared Pearson residuals produces the Pearson Chi-squared statistic:

$$\chi ^2 = \sum_i r_i^2$$

Deviance residuals for logistic regression

• Deviance residuals and Pearson residuals converge for high degrees of freedom
• Deviance residuals indicate the contribution of each point to the model likelihood
• Definition of deviance residuals:

$$d_i = s_i \sqrt{ -2 ( y_i \log \hat y_i + (1-y_i) \log (1 - \hat y_i) ) }$$

Where $s_i = 1$ if $y_i = 1$ and $s_i = -1$ if $y_i = 0$.

• Summing the deviances gives the overall deviance: $D = \sum_i d_i^2$

Likelihood and hypothesis testing

What is likelihood?

• The likelihood of a model is the probability of the observed outcomes given the model, sometimes written as:
  • $L(\theta | data) = P(data|\theta)$.
• Deviance residuals and the difference in log-likelihood between two models are related by:

$\Delta (\textrm{D}) = -2 * \Delta (\textrm{log likelihood})$

Likelihood Ratio Test

• Use to assess whether the reduction in deviance provided by a more complicated model indicates a better fit
• It is equivalent of the nested Analysis of Variance is a nested Analysis of Deviance
• The difference in deviance under $H_0$ is chi-square distributed, with df equal to the difference in df of the two models.

Likelihood Ratio Test (cont’d)

fit0 <- glm(cbind(using, notUsing) ~ -1, data=cuse, 
            family=binomial("logit"))
anova(fit0, fit1, test="LRT")

## Analysis of Deviance Table
## 
## Model 1: cbind(using, notUsing) ~ -1
## Model 2: cbind(using, notUsing) ~ age + education + wantsMore
##   Resid. Df Resid. Dev Df Deviance  Pr(>Chi)    
## 1        16     389.85                          
## 2        10      29.92  6   359.94 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Wald test for individual regression coefficients

• Can use partial Wald test for a single coefficient:
  • $\frac{\hat{\beta}}{\sqrt{var(\hat{\beta)}}} \sim t_{n-1}$
  • $\frac{\left ( \hat{\beta} - \beta_0 \right )^2 }{var(\hat{\beta)}} \sim \chi^2_{df=1}$ (large sample)
• Wald CI for $\beta$: $\hat{\beta} \pm t_{1-\alpha/2, n-1} \sqrt{var(\hat{\beta})}$
• Wald CI for odds-ratio: $e^{\hat{\beta} \pm t_{1-\alpha/2, n-1} \sqrt{var(\hat{\beta})}}$

Note: Wald test confidence intervals on coefficients can provide poor coverage in some cases, even with relatively large samples

Additive vs. Multiplicative models

Additive vs. Multiplicative models

• Linear regression is an additive model
  • e.g. for two binary variables $\beta_1 = 1.5$, $\beta_2 = 1.5$.
  • If $x_1=1$ and $x_2=1$, this adds 3.0 to $E(y|x)$
• Logistic regression is a multiplicative model
  • If $x_1=1$ and $x_2=1$, this adds 3.0 to $log(\frac{P}{1-P})$
  • Odds-ratio $\frac{P}{1-P}$ increases 20-fold: $exp(1.5+1.5)$ or $exp(1.5) * exp(1.5)$