Session 10: Repeated Measures and Longitudinal Analysis II

Levi Waldron

Source: vignettes/session_lecture.Rmd

Learning objectives and outline

Learning objectives

  1. Define mixed effects models and population average models
  2. Perform model diagnostics for random effects models
  3. Interpret random intercepts and random slopes
  4. Define and perform population average models
  5. Define assumptions on correlation structure in hierarchical models
  6. Choose between hierarchical modeling strategies

Outline

  1. Review of fecal fat dataset
  2. Summary of non-hierarchical approaches
  3. Mixed effects models
  4. Longitudinal data and the Georgia Birthweights dataset
  5. Population average models and Generalized Estimating Equations (GEE)
  • Vittinghoff sections 7.2, 7.3, 7.5

Review

Fecal fat dataset

  • Lack of digestive enzymes in the intestine can cause bowel absorption problems.
    • This will be indicated by excess fat in the feces.
    • Pancreatic enzyme supplements can alleviate the problem.
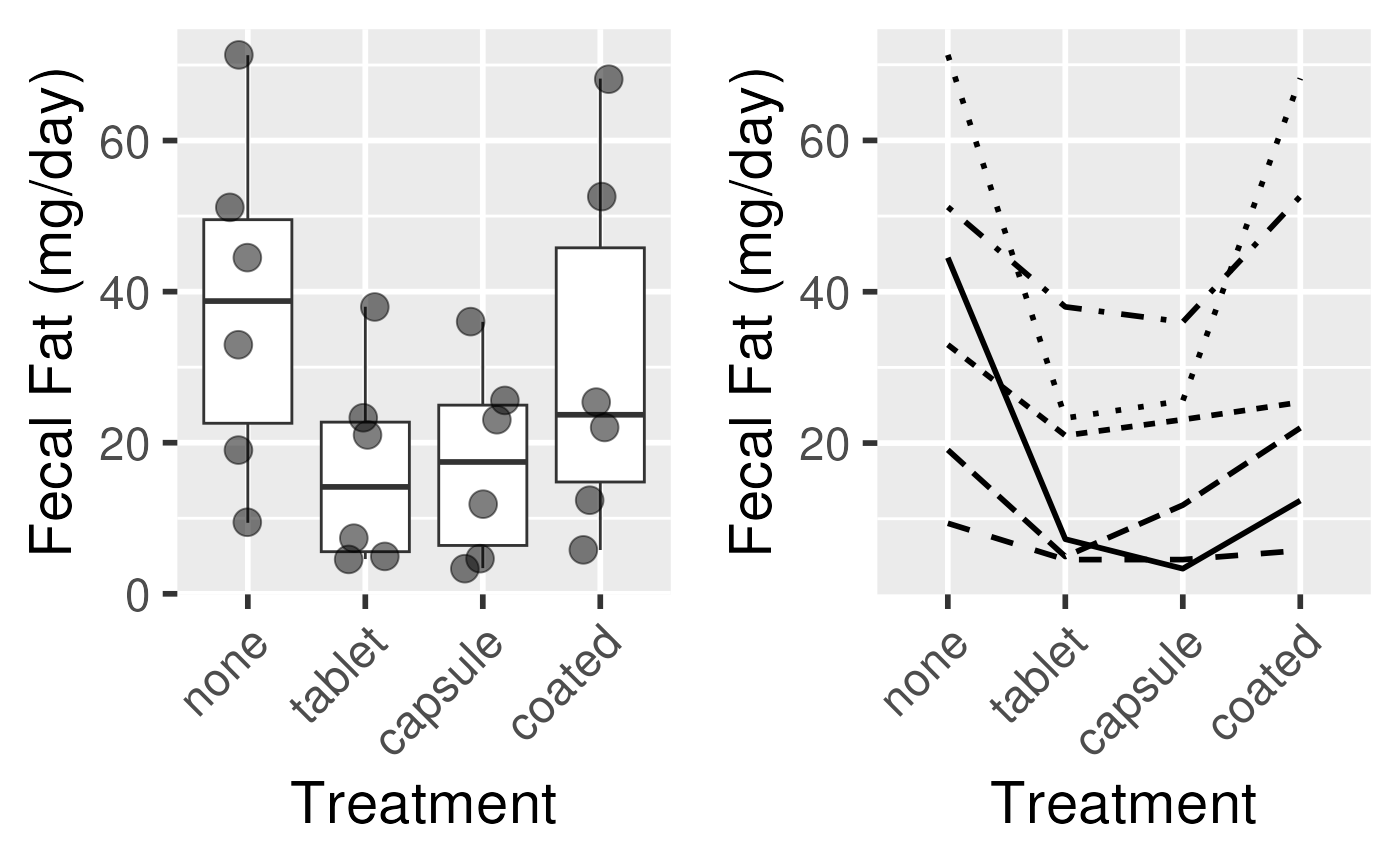
    • fecfat.csv: a study of fecal fat quantity (g/day) for individuals given each of a placebo and 3 types of pills
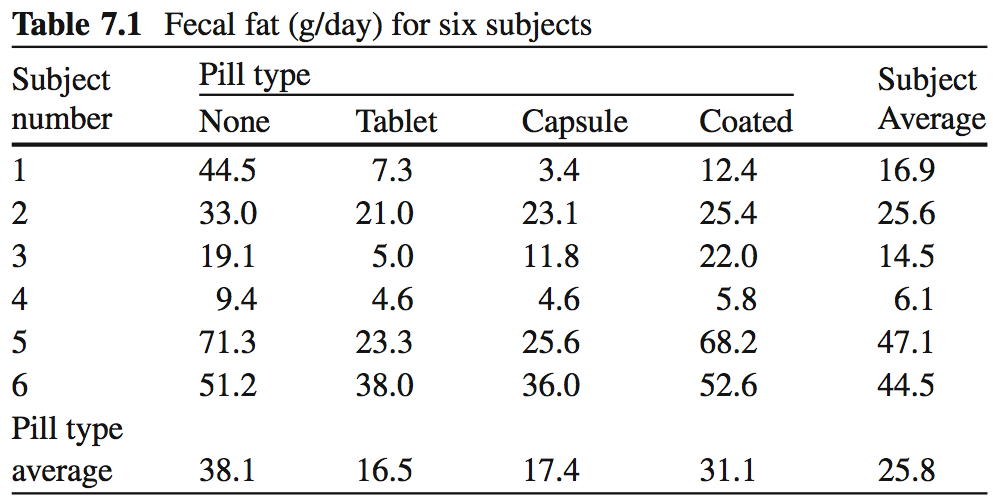
Fecal Fat dataset
Fecal Fat dataset

Fecal fat dataset 

## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.

Analysis strategies for hierarchical data

  • Fixed effects and other non-hierarchical strategies
  • Random / mixed effects models
    • model certain regression coefficients (intercept, slopes) as random variables
  • Population average models
    • using Generalized Estimating Equations (GEE)

Non-hierarchical analysis strategies

Non-hierarchical analysis strategies for hierarchical data

  • Analyses for each subgroup
    • e.g., look at each patient independently
    • doesn’t work at all in this example, and in general is not an integrated analysis of the whole data
    • could sort of work for an example with many patients per doctor, a few doctors
  • Analysis at the highest level in the hierarchy
    • first summarize data to highest level
    • doesn’t work at all in this example
    • could sort of work for an example with few patients per doctor, many doctors
  • Analysis on “Derived Variables”
    • consider each treatment type separately, take differences in fat levels between treatment/control for each patient and use paired t-tests
    • can work, but not for unbalanced groups
  • Fixed-effects models

When is hierarchical analysis definitely needed?

  1. the correlation structure is of interest, e.g. familial aggregation of disease, or consistency of treatment within centers
  2. we wish to “borrow strength” across the levels of a hierarchy in order to improve estimates
  3. dealing with unbalanced data
  4. we want to benefit from software designed for hierarchical data

Mixed effects models

Mixed effects models

  • Model looks like two-way ANOVA: \[ FECFAT_{ij} = \beta_0 + \beta_{subject i} SUBJECT_i + \beta_{pilltype j} PILLTYPE_j + \epsilon_{ij} \]
    • Assumption: \(\epsilon_i \stackrel{iid}{\sim} N(0, \sigma_\epsilon^2)\)
  • But instead of fitting a \(\beta\) to each individual, we assume that the subject effects are selected from a distribution of possible subject effects: \[ FECFAT_{ij} = \beta_0 + SUBJECT_i + \beta_{pilltype j} PILLTYPE_j + \epsilon_{ij} \]

Where we assume: \(SUBJECT_i \stackrel{iid}{\sim} N(0, \tau_{00}^2)\)

  • This is a mixed effects model because:
    • the “true” intercept varies randomly from patient to patient
    • the “true” (population) coefficient of treatment is fixed (the same for everyone)

Fit this mixed-effects model 

library(nlme)
fitmix <- nlme::lme(fecfat ~ pilltype, 
                    data = dat, 
                    random =  ~ 1 | subject)

Note: the lme4 package is another popular alternative

Mixed effects model coeffients, variances, ICC 

## Linear mixed-effects model fit by REML
##   Data: dat 
##   Log-restricted-likelihood: -84.55594
##   Fixed: fecfat ~ pilltype 
##     (Intercept)  pilltypetablet pilltypecapsule  pilltypecoated 
##       38.083334      -21.550001      -20.666667       -7.016668 
## 
## Random effects:
##  Formula: ~1 | subject
##         (Intercept) Residual
## StdDev:    15.89557 10.34403
## 
## Number of Observations: 24
## Number of Groups: 6

\(ICC = 15.9^2 / (15.9^2 + 10.34^2)\) = 0.7 = 0.7.

  • Recall ICC is a measure of how large the subject effect is, in relation to the error term
  • Variances were estimated directly by the model!

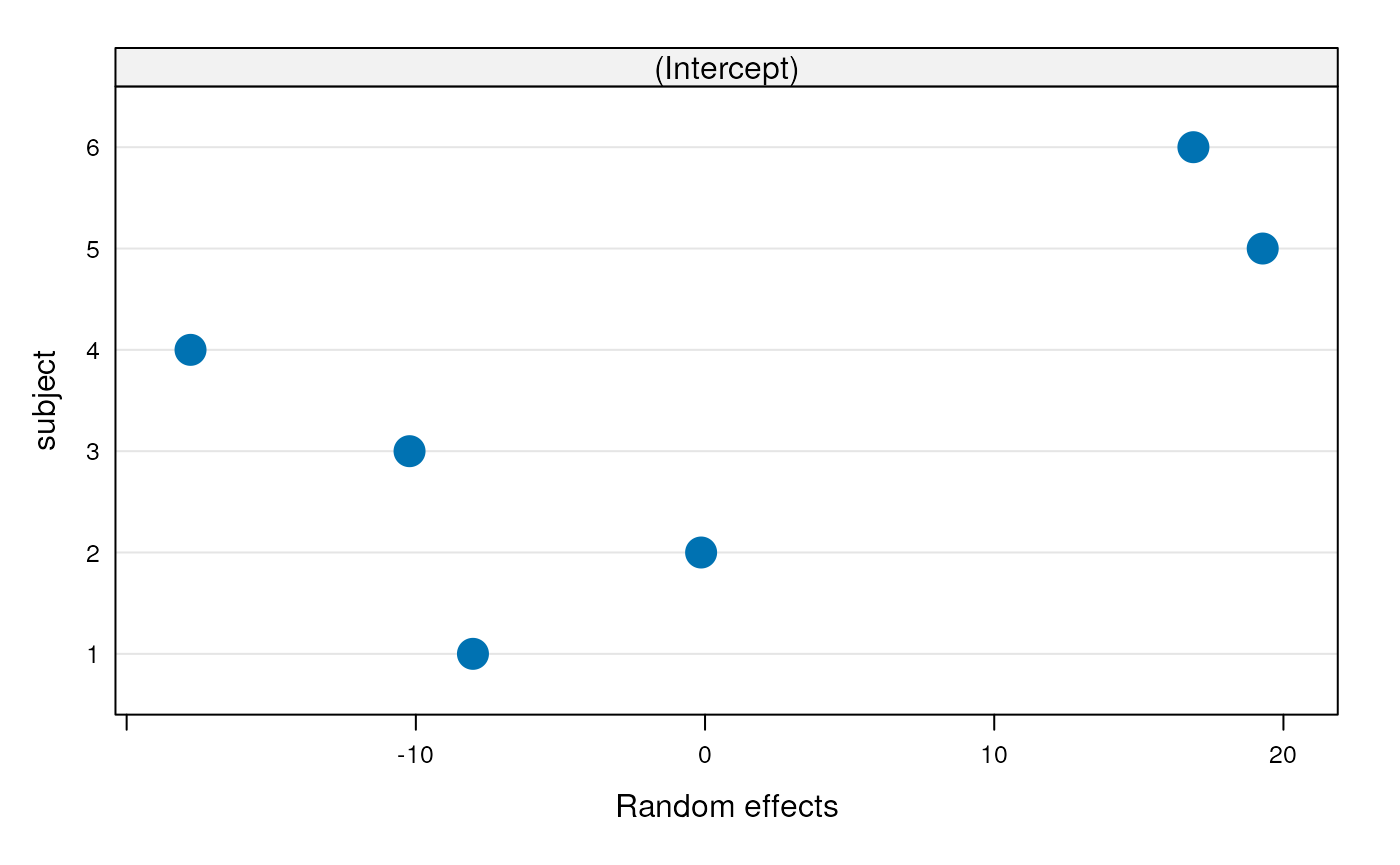
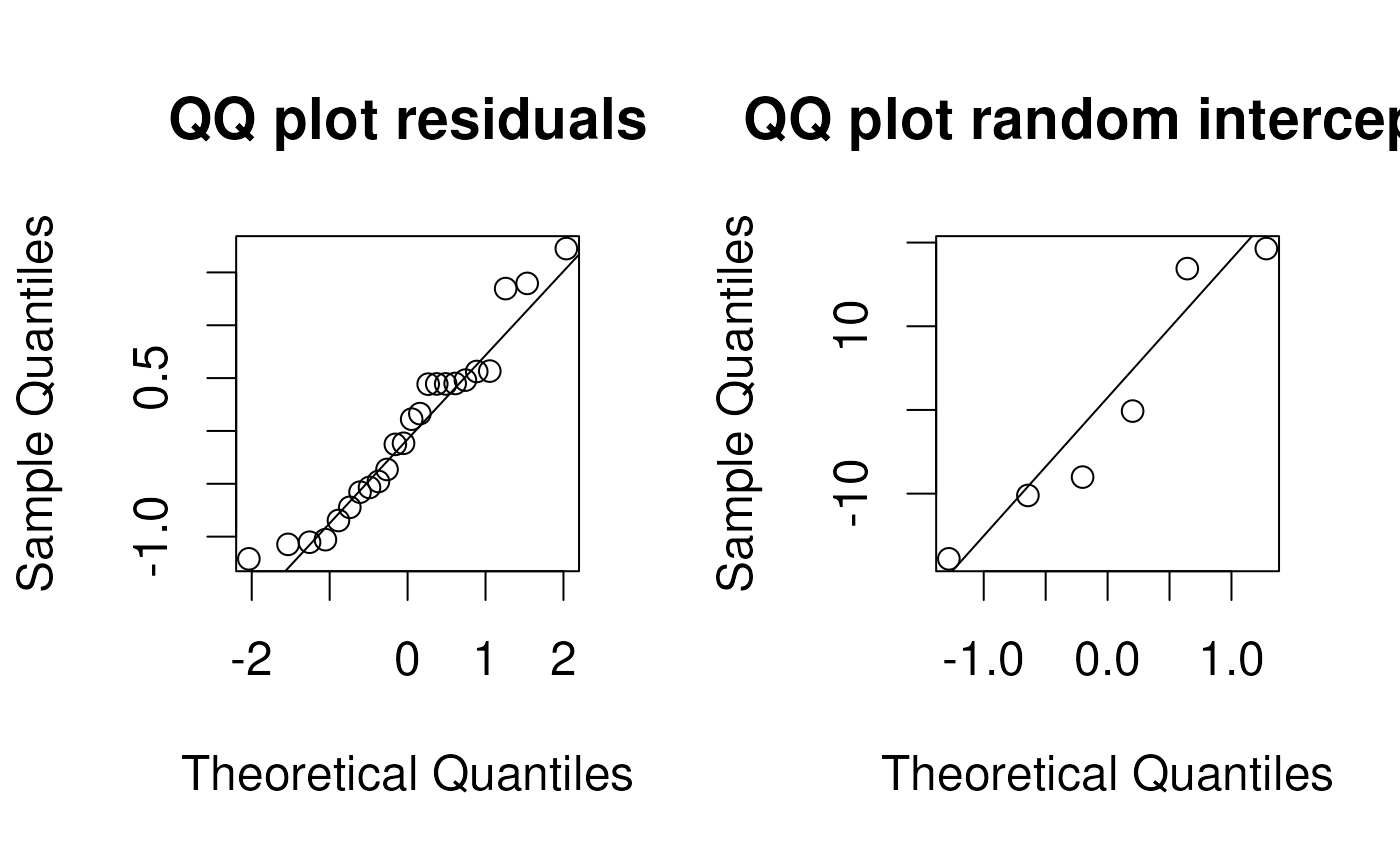
Assumptions of the mixed model

\[ FECFAT_{ij} = \beta_0 + SUBJECT_i + \beta_{pilltype j} PILLTYPE_j + \epsilon_{ij} \]

  • Normally distributed residuals as in fixed effects model:
    • \(\epsilon_i \stackrel{iid}{\sim} N(0, \sigma_\epsilon^2)\)
  • Normally distributed latent variable:
    • \(SUBJECT_i \stackrel{iid}{\sim} N(0, \tau_{00}^2)\)

Mixed effects model results

A plot of the random intercept:

Mixed effects model diagnostics

``

Mixed effects model results 

## Linear mixed-effects model fit by REML
##   Data: dat 
##        AIC      BIC    logLik
##   181.1119 187.0863 -84.55594
## 
## Random effects:
##  Formula: ~1 | subject
##         (Intercept) Residual
## StdDev:    15.89557 10.34403
## 
## Fixed effects:  fecfat ~ pilltype 
##                     Value Std.Error DF   t-value p-value
## (Intercept)      38.08333  7.742396 15  4.918805  0.0002
## pilltypetablet  -21.55000  5.972127 15 -3.608430  0.0026
## pilltypecapsule -20.66667  5.972127 15 -3.460521  0.0035
## pilltypecoated   -7.01667  5.972127 15 -1.174903  0.2583
##  Correlation: 
##                 (Intr) plltypt plltypcp
## pilltypetablet  -0.386                 
## pilltypecapsule -0.386  0.500          
## pilltypecoated  -0.386  0.500   0.500  
## 
## Standardized Within-Group Residuals:
##          Min           Q1          Med           Q3          Max 
## -1.210052934 -0.615068039 -0.002727166  0.457105344  1.725618643 
## 
## Number of Observations: 24
## Number of Groups: 6
  • Note: correlation of the estimator of the fixed effects
    • high correlations may (but not necessarily) be due to collinearity
    • not usually useful, not included in output of some packages

Mixed effects model results

Inference for variance terms (and fixed effects): 

## Approximate 95% confidence intervals
## 
##  Fixed effects:
##                     lower       est.     upper
## (Intercept)      21.58081  38.083334 54.585860
## pilltypetablet  -34.27929 -21.550001 -8.820714
## pilltypecapsule -33.39595 -20.666667 -7.937381
## pilltypecoated  -19.74595  -7.016668  5.712618
## 
##  Random Effects:
##   Level: subject 
##                   lower     est.    upper
## sd((Intercept)) 8.00117 15.89557 31.57904
## 
##  Within-group standard error:
##    lower     est.    upper 
##  7.23240 10.34403 14.79438
  • Would conclude that variation of the intercept between subjects is non-zero
    • not attributable to within-subject variation

Longitudinal data

Longitudinal data

  • Interested in the change in the value of a variable within a “subject”
  • Collect data repeatedly through time.
  • For hierarchical longitudinal analysis to be effective, before/after measurements need to be positively correlated

Longitudinal data

  • Interested in the change in the value of a variable within a “subject”
  • Collect data repeatedly through time.
  • For hierarchical longitudinal analysis to be effective, before/after measurements need to be positively correlated

Longitudinal data examples

  • Example 1: a measure of sleepiness before and after administration of treatment or placebo
  • Example 2: Study of Osteoporotic Fractores (SOF dataset)
    • 9,704 women tracked with clinical visits every two years
    • Bone Mineral Density (BMD), Body Mass Index (BMI), many other variables
  • Questions for Example 2:
    1. Is change in BMD related to age at menopause? This is a time-invariant predictor, age at menopause, with time-dependent changes in the outcome, BMD.
    2. Is change in BMD related to change in BMI? This is an analysis relating a time-varying predictor, BMI, with changes in the outcome, BMD. BMI varies quite a lot between women, but also varies within a woman over time.

Longitudinal data examples

  • birthweight and birth order
  • provides birthweights and order of infants from mothers who had 5 children in Georgia
    • interested in whether birthweight of babies changes with order
    • whether this difference depends on the mother’s age at first childbirth or on the weight of initial baby.

Georgia Birthweights dataset

Boxplot and “Spaghetti” plot:

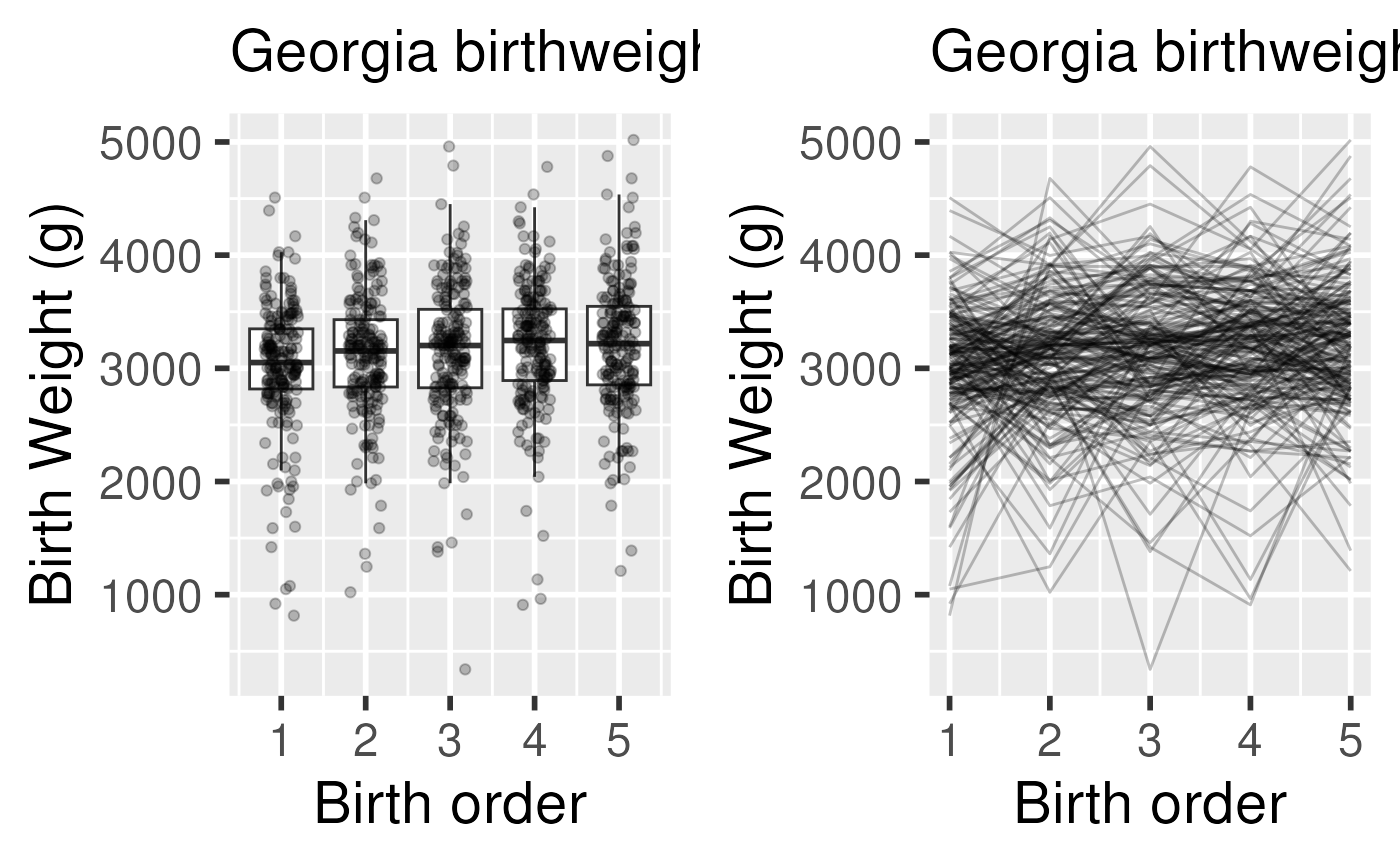
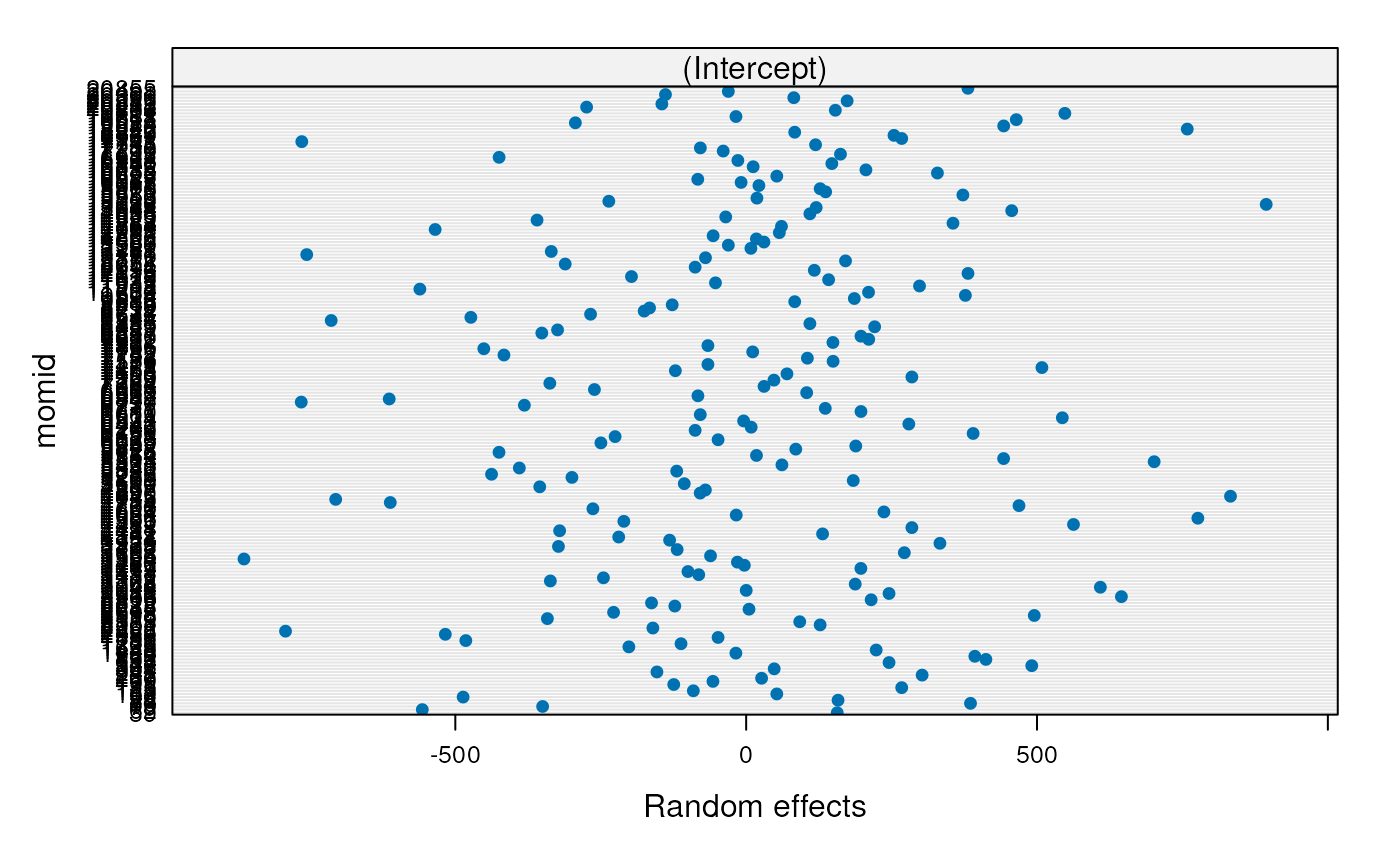
Georgia Birthweights dataset

  • Does baseline birth weight vary by mother?
    • random intercept
library(nlme)
gafit1 <- lme(bweight ~ birthord, data=ga, 
              random=~1|momid)

Note: there are not enough degrees of freedom to also fit a random coefficient for birth order

Georgia Birthweights dataset

Georgia Birthweights dataset 

summary(gafit1)
## Linear mixed-effects model fit by REML
##   Data: ga 
##        AIC      BIC    logLik
##   15321.65 15341.28 -7656.826
## 
## Random effects:
##  Formula: ~1 | momid
##         (Intercept) Residual
## StdDev:    367.2676 445.0228
## 
## Fixed effects:  bweight ~ birthord 
##                Value Std.Error  DF  t-value p-value
## (Intercept) 2995.640  41.99615 799 71.33130       0
## birthord      46.608   9.95101 799  4.68374       0
##  Correlation: 
##          (Intr)
## birthord -0.711
## 
## Standardized Within-Group Residuals:
##         Min          Q1         Med          Q3         Max 
## -5.26801358 -0.43683345  0.05028638  0.52703429  3.30770805 
## 
## Number of Observations: 1000
## Number of Groups: 200

Georgia Birthweights dataset 

intervals(gafit1, which = "all")
## Approximate 95% confidence intervals
## 
##  Fixed effects:
##                  lower     est.      upper
## (Intercept) 2913.20418 2995.640 3078.07582
## birthord      27.07478   46.608   66.14122
## 
##  Random Effects:
##   Level: momid 
##                    lower     est.    upper
## sd((Intercept)) 323.1724 367.2676 417.3794
## 
##  Within-group standard error:
##    lower     est.    upper 
## 423.7298 445.0228 467.3859
  • Does baseline birth weight vary by mother?
    • yes: the subject variance is significantly greater than zero
    • The variance between mothers is too much to be explained by within-mother variation in birth weights

Population Average Models

Population Average Models

  • An alternative to random / mixed-effects models that is more robust to assumptions of:
    • distribution of random effects
    • correlation structure
  • Estimates correlation structure from the data rather than assuming normality
    • Requires more clusters than observations per cluster
  • Estimates regression coefficients and robust standard errors
    • commonly by Generalized Estimating Equations (GEE)

Population Average Models

  • Compare mixed model multiple linear regression: \[ E[Y_{ij}|X_{ij}] = \beta_0 + \alpha_{0j} + \beta_1 X_{ij}, \alpha_{0j} \sim N(0, \sigma) \] for subject \(i\) in group \(j\).

  • to a population average model: \[ E[Y_{ij}|X_{ij}] = \beta_0^* + \beta_1^* X_{ij} \]

  • Interpretations of \(\beta^*\) and \(\beta\) are equivalent

  • Numerically equivalent for linear and log-linear models (if specification of mixed model is correct), but not for logistic link.

Fit a population average model 

gafit.gee <- gee::gee(bweight ~ birthord,
                      corstr = "exchangeable",
                      id = momid,
                      data = ga)

summary(gafit.gee)
## 
##  GEE:  GENERALIZED LINEAR MODELS FOR DEPENDENT DATA
##  gee S-function, version 4.13 modified 98/01/27 (1998) 
## 
## Model:
##  Link:                      Identity 
##  Variance to Mean Relation: Gaussian 
##  Correlation Structure:     Exchangeable 
## 
## Call:
## gee::gee(formula = bweight ~ birthord, id = momid, data = ga, 
##     corstr = "exchangeable")
## 
## Summary of Residuals:
##       Min        1Q    Median        3Q       Max 
## -2795.464  -299.126    48.840   341.144  1824.536 
## 
## 
## Coefficients:
##             Estimate Naive S.E.   Naive z Robust S.E.  Robust z
## (Intercept) 2995.640  41.973695 71.369462   38.808066 77.191170
## birthord      46.608   9.958128  4.680398    9.996256  4.662546
## 
## Estimated Scale Parameter:  332525.3
## Number of Iterations:  1
## 
## Working Correlation
##           [,1]      [,2]      [,3]      [,4]      [,5]
## [1,] 1.0000000 0.4035684 0.4035684 0.4035684 0.4035684
## [2,] 0.4035684 1.0000000 0.4035684 0.4035684 0.4035684
## [3,] 0.4035684 0.4035684 1.0000000 0.4035684 0.4035684
## [4,] 0.4035684 0.4035684 0.4035684 1.0000000 0.4035684
## [5,] 0.4035684 0.4035684 0.4035684 0.4035684 1.0000000

Correlation assumptions for GEE

Must make some assumption about the form of correlation among grouped observations. Some options are:

  • Independence:
    • no correlation between measurements within group
  • Exchangeable:
    • all pairwise correlations are the same (in large-N limit)
    • nothing distinguishes one member of a cluster from another
    • appropriate in the absence of other data structures such as measurements taken through time or space
  • Auto-regressive (AR-M):
    • observations taken more closely in time are more highly correlated

Correlation assumptions for GEE (cont’d)

  • Unstructured:
    • estimates a separate correlation between observations taken on each pair of “times”
  • Non-stationary (“non_stat_M_dep”):
    • similar to unstructured, but assumes all correlations for pairs separated far enough in time are zero
  • Stationary (“stat_M_dep”):
    • e.g. stationary of order 2: observations taken at time points 1 and 3 have the same correlation as time points 2 and 4
    • but this might be different from the correlation between observations taken at times 2 and 3
    • correlations for observations 3 or more time periods apart assumed to be zero

Fewer assumptions requires more data, and good assumptions improve results

Help in choosing a method

Hierarchical modeling decision table from Moen et al.
Hierarchical modeling decision table from Moen et al.

Conclusions

  • Ignoring within-subject correlations can produce very wrong results, and is not always “conservative”
  • Hierarchical analysis strategies are needed for any of:
    1. When the correlation structure is of primary interest, e.g. familial aggregation of disease, or consistency of treatment within centers,
    2. When we wish to “borrow strength” across the levels of a hierarchy in order to improve estimates, and
    3. When dealing with unbalanced correlated data. E.g., no requirement that each Georgia mother have exactly 5 children.
  • Population average models provide a robust alternative to mixed models
    • for one level of hierarchy

A final note on reporting results of hypothesis tests

  • Include test statistic, a measure of “effect size”, and test name if unclear from test statistic
  • Write in plain language and let the statistics support, not lead. E.g.:
    • do: The 36 study participants had a mean age of 27.4 (SD = 12.6), significantly older than the university mean of 21.2 years (t(35) = 2.95, p = 0.01).
    • don’t: A p-value of 0.01 indicated significant difference in age of study participants compared to all university students.
    • do: report confidence intervals where possible

CONGRATULATIONS!!!